|
|
| Línea 2: |
Línea 2: |
| | | | |
| | == (Jueves 2-IV-2009) Marco Antonio Fontelos, ICMAT (CSIC) == | | == (Jueves 2-IV-2009) Marco Antonio Fontelos, ICMAT (CSIC) == |
| - | '''Singularidades en fluídos perfectos incompresibles con frontera libre: ruptura de olas y formación de burbujas''' | + | '''Singularidades en fluídos perfectos incompresibles con frontera |
| | + | libre: ruptura de olas y formación de burbujas''' |
| | | | |
| - | '''Resumen:''' El fenómeno de formación de singularidades es particularmente llamativo en varios problemas de mecánica de fluídos como son la ruptura de una columna de aire en agua para formar burbujas o la ruptura de una ola. En la charla presentaremos la formulación matemática de estos problemas, así como algunos progresos recientes en el análisis de la estructura de sus singularidades que, como veremos, pueden presentar forma autosimilar pero con exponentes anómalos. [[Material_adicional]] | + | '''Resumen:''' El fenómeno de formación de singularidades es |
| | + | particularmente llamativo en varios problemas de mecánica de fluídos |
| | + | como son la ruptura de una columna de aire en agua para formar |
| | + | burbujas o la ruptura de una ola. En la charla presentaremos la |
| | + | formulación matemática de estos problemas, así como algunos progresos |
| | + | recientes en el análisis de la estructura de sus singularidades que, |
| | + | como veremos, pueden presentar forma autosimilar pero con exponentes |
| | + | anómalos. [[Material_adicional]] |
| | | | |
| - | Jueves 2 de abril 2009, 12:00-13:00, Aula QC22, (planta 2 del pabellón C (aulario), Facultad de Ciencias Químicas, UCM) | + | Jueves 2 de abril 2009, 12:00-13:00, Aula QC22, (planta 2 del |
| | + | pabellón C (aulario), Facultad de Ciencias Químicas, UCM) |
| | | | |
| - | == (Viernes 17-IV-2009), Valentin García Baonza, Dept de Química Física, UCM == | + | == (Viernes 17-IV-2009), Valentin García Baonza, Dept de Química |
| | + | Física, UCM == |
| | | | |
| - | ''' Retos matemáticos en aplicaciones científico-tecnológicas: el caso de la alta presión,''' | + | ''' Retos matemáticos en aplicaciones científico-tecnológicas: el caso |
| | + | de la alta presión,''' |
| | | | |
| - | '''Resumen:''' La búsqueda de sinergias entre científicos de diferentes áreas es un importante reto en numerosas aplicaciones científicas y/o tecnológicas. Este hecho es especialmente urgente en líneas de investigación incipientes que, en muchos casos, son escasamente conocidas incluso por científicos de campos afines. En este seminario se expondrá de forma clara y concisa la problemática asociada a fenómenos que tienen lugar a altas presiones. Esta tecnología de futuro todavía necesita resolver algunos problemas metodológicos que se verían enormemente simplificados con el empleo de métodos matemáticos modernos y simulaciones computacionales. Se trata, en definitiva de acercar esta rama científica multidisciplinar al mundo de las matemáticas, intentando de detectar aquellos casos científicos donde la aplicación de los métodos matemáticos sea más significativa. | + | '''Resumen:''' La búsqueda de sinergias entre científicos de |
| | + | diferentes áreas es un importante reto en numerosas aplicaciones |
| | + | científicas y/o tecnológicas. Este hecho es especialmente urgente en |
| | + | líneas de investigación incipientes que, en muchos casos, son |
| | + | escasamente conocidas incluso por científicos de campos afines. En |
| | + | este seminario se expondrá de forma clara y concisa la problemática |
| | + | asociada a fenómenos que tienen lugar a altas presiones. Esta |
| | + | tecnología de futuro todavía necesita resolver algunos problemas |
| | + | metodológicos que se verían enormemente simplificados con el empleo de |
| | + | métodos matemáticos modernos y simulaciones computacionales. Se trata, |
| | + | en definitiva de acercar esta rama científica multidisciplinar al |
| | + | mundo de las matemáticas, intentando de detectar aquellos casos |
| | + | científicos donde la aplicación de los métodos matemáticos sea más |
| | + | significativa. |
| | [[Material_adicional]] | | [[Material_adicional]] |
| | | | |
| - | Viernes 17 de abril, 13:00-14:00, Aula QB63 (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) | + | Viernes 17 de abril, 13:00-14:00, Aula QB63 (planta 6 del |
| | + | pabellón B, Facultad de Ciencias Químicas, UCM) |
| | | | |
| | + | == (Viernes 24-IV-2009) José M. Mazón Ruiz, Departamento de Análisis |
| | + | Matemático, Univ Valencia == |
| | | | |
| - | == (Viernes 24-IV-2009) José M. Mazón Ruiz, Departamento de Análisis Matemático, Univ Valencia ==
| + | ''' Ecuaciones en derivadas parciales gobernadas por operadores |
| | + | acretivos''' |
| | | | |
| - | ''' Ecuaciones en derivadas parciales gobernadas por operadores acretivos''' | + | '''Resumen:''' Una teoría que ha resultado de gran utilidad en el |
| | + | estudio de algunas ecuaciones en derivadas parciales no lineales es la |
| | + | teoría de semigrupos no lineales generados por operadores acretivos en |
| | + | espacios de Banach, basada fundamentalmente en el Teorema de |
| | + | Crandall-Ligget y las aporataciones de Ph. Bénilan. En esta charla, |
| | + | después de hacer unaexposición esquemática de esta teoría general, |
| | + | veremos con se aplica a algunas importantes ecuaciones en derivadas |
| | + | parciales no lineales. |
| | | | |
| - | '''Resumen:''' Una teoría que ha resultado de gran utilidad en el estudio de algunas ecuaciones en derivadas parciales no lineales es la teoría de semigrupos no lineales generados por operadores acretivos en espacios de Banach, basada fundamentalmente en el Teorema de Crandall-Ligget y las aporataciones de Ph. Bénilan. En esta charla, después de hacer unaexposición esquemática de esta teoría general, veremos con se aplica a algunas importantes ecuaciones en derivadas parciales no lineales.
| + | Viernes 24 de abril, 13:00-14:00, Aula QB63 (planta 6 del pabellón |
| | + | B, Facultad de Ciencias Químicas, UCM) |
| | | | |
| - | Viernes 24 de abril, 13:00-14:00, Aula QB63 (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM)
| + | == (Jueves 30-IV-2009) Angela Jiménez Casas, Universidad Pontificia |
| | + | Comillas de Madrid== |
| | | | |
| - | == (Jueves 30-IV-2009) Angela Jiménez Casas, Universidad Pontificia Comillas de Madrid==
| + | ''' Asymptotic behaviour for small width of interface in phase-field |
| - | | + | model''' |
| - | ''' Asymptotic behaviour for small width of interface in phase-field model''' | + | |
| | | | |
| - | '''Abstract:''' We consider a generalization of the semilinear phase field model from [1], by using a more general density function which describe the phase separation of mixtures of three or more components, instead of binary mixtures. The main objective of this work is to prove the existence of metastable solutions that evolve very slowly in time, for this general model. | + | '''Abstract:''' We consider a generalization of the semilinear phase |
| | + | field model from [1], by using a more general density function which |
| | + | describe the phase separation of mixtures of three or more components, |
| | + | instead of binary mixtures. The main objective of this work is to |
| | + | prove the existence of metastable solutions that evolve very slowly in |
| | + | time, for this general model. |
| | | | |
| - | Finally we consider a general enthalpy function which allows to study more general couplings between a diffusion field and a phase-field. For instance, the phase field can be seen as the density of bacterial collony or the mass of growing tumor. Analogously, the diffusion field can stand for the density of nutrient. In this case we prove also the existence of the metastable solutions of the generalized system. | + | Finally we consider a general enthalpy function which allows to study |
| | + | more general couplings between a diffusion field and a phase-field. |
| | + | For instance, the phase field can be seen as the density of bacterial |
| | + | collony or the mass of growing tumor. Analogously, the diffusion field |
| | + | can stand for the density of nutrient. In this case we prove also the |
| | + | existence of the metastable solutions of the generalized system. |
| | [[Material_adicional]] | | [[Material_adicional]] |
| | | | |
| - | Jueves 30 de abril, 13:00-14:00, Aula QB63 (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) | + | Jueves 30 de abril, 13:00-14:00, Aula QB63 (planta 6 del |
| | + | pabellón B, Facultad de Ciencias Químicas, UCM) |
| | | | |
| - | [1] A. Jiménez-Casas, A. Rodriguez-Bernal, Linear stabilility analysis and metastable solutions for a phase-field model, Proceeding of the Royal Society of Edimburgh, 129A,571- 600, (1999). | + | [1] A. Jiménez-Casas, A. Rodriguez-Bernal, Linear stabilility analysis |
| | + | and metastable solutions for a phase-field model, Proceeding of the |
| | + | Royal Society of Edimburgh, 129A,571- 600, (1999). |
| | | | |
| | == (Viernes 8-V-2009) Anxo Sánchez, Universidad Carlos III de Madrid == | | == (Viernes 8-V-2009) Anxo Sánchez, Universidad Carlos III de Madrid == |
| | | | |
| - | ''' Resultados recientes sobre teoría evolutiva de juegos en grafos: complejidad y ausencia de universalidad ''' | + | ''' Resultados recientes sobre teoría evolutiva de juegos en grafos: |
| | + | complejidad y ausencia de universalidad ''' |
| | | | |
| - | '''Resumen:''' En esta charla presentaré una panorámica de los resultados sobre teoría evolutiva de juegos en grafos que se han obtenido a partir del trabajo pionero de Nowak y May en 1992. Tras una introducción a la teoría de juegos evolutiva, entraré a discutir los resultados basándome en un amplio programa de simulaciones que cubren distintos aspectos del problema. Incidiré en las principales diferencias que se observan con respecto a la situación "bien mezclada" o "de campo medio" así como en los distintos comportamientos asintóticos que aparecen al cambiar los ingredientes de los modelos. Concluiré enmarcando los resultados en el campo de los sistemas complejos, haciendo hincapié en los problemas de ausencia de universalidad, y plantearé algunas cuestiones abiertas. [[Material_adicional]] | + | '''Resumen:''' En esta charla presentaré una panorámica de los |
| | + | resultados sobre teoría evolutiva de juegos en grafos que se han |
| | + | obtenido a partir del trabajo pionero de Nowak y May en 1992. Tras una |
| | + | introducción a la teoría de juegos evolutiva, entraré a discutir los |
| | + | resultados basándome en un amplio programa de simulaciones que cubren |
| | + | distintos aspectos del problema. Incidiré en las principales |
| | + | diferencias que se observan con respecto a la situación "bien |
| | + | mezclada" o "de campo medio" así como en los distintos comportamientos |
| | + | asintóticos que aparecen al cambiar los ingredientes de los modelos. |
| | + | Concluiré enmarcando los resultados en el campo de los sistemas |
| | + | complejos, haciendo hincapié en los problemas de ausencia de |
| | + | universalidad, y plantearé algunas cuestiones abiertas. |
| | + | [[Material_adicional]] |
| | | | |
| | | | |
| - | Viernes 8 de mayo, 13:00-14:00, Aula QB63 (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) | + | Viernes 8 de mayo, 13:00-14:00, Aula QB63 (planta 6 del pabellón |
| | + | B, Facultad de Ciencias Químicas, UCM) |
| | | | |
| | == (Jueves 14-V-2009) Marcone C. Pereira, Universidade de Sao Paulo == | | == (Jueves 14-V-2009) Marcone C. Pereira, Universidade de Sao Paulo == |
| Línea 52: |
Línea 115: |
| | ''' Dominios finos con oscilaciones ''' | | ''' Dominios finos con oscilaciones ''' |
| | | | |
| - | '''Resumen: ''' En esta charla consideramos la investigación del comportamiento asintótico de las soluciones del problema de Newmann para el operador de Laplace en dominios finos con oscilaciones en la frontera. Para ello, hemos seguido el método de múltiples escalas (como lo hace Cioranescu & Saint Jean Paulin en [1]) y hemos obtenido resultados de convergencia por el método de energía introducido por Tartar en [2] and [3]. | + | '''Resumen: ''' En esta charla consideramos la investigación del |
| | + | comportamiento asintótico de las soluciones del problema de Newmann |
| | + | para el operador de Laplace en dominios finos con oscilaciones en la |
| | + | frontera. Para ello, hemos seguido el método de múltiples escalas |
| | + | (como lo hace Cioranescu & Saint Jean Paulin en [1]) y hemos obtenido |
| | + | resultados de convergencia por el método de energía introducido por |
| | + | Tartar en [2] and [3]. |
| | | | |
| | Referencias | | Referencias |
| | | | |
| - | [1] Cioranescu, D. and Saint J. Paulin, J; Homogenization of Reticulated Structures, Springer | + | [1] Cioranescu, D. and Saint J. Paulin, J; Homogenization of |
| | + | Reticulated Structures, Springer |
| | Verlag (1980). | | Verlag (1980). |
| | | | |
| - | [2] L. Tartar; Probl`emmes d’homogénéisation dans les équations aux dérivées partielles, Cours | + | [2] L. Tartar; Probl`emmes d’homogénéisation dans les équations aux |
| | + | dérivées partielles, Cours |
| | Peccot, Coll`ege de France (1977). | | Peccot, Coll`ege de France (1977). |
| | | | |
| - | [3] L. Tartar; Quelques remarques sur l´homegénéisation, Function Analysis and Numerical | + | [3] L. Tartar; Quelques remarques sur l´homegénéisation, Function |
| - | Analysis, Proc. Japan-France Seminar 1976, ed. H. Fujita, Japanese Society for the Promotion | + | Analysis and Numerical |
| | + | Analysis, Proc. Japan-France Seminar 1976, ed. H. Fujita, Japanese |
| | + | Society for the Promotion |
| | of Science, 468-482 (1978). | | of Science, 468-482 (1978). |
| | | | |
| - | Jueves 14 de mayo, 12:00-13:00, Aula QB63 (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) | + | Jueves 14 de mayo, 12:00-13:00, Aula QB63 (planta 6 del pabellón |
| | + | B, Facultad de Ciencias Químicas, UCM) |
| | | | |
| | (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) | | (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) |
| Línea 72: |
Línea 146: |
| | == (Viernes 22-V-2009) R. Quintanilla, UPC== | | == (Viernes 22-V-2009) R. Quintanilla, UPC== |
| | | | |
| - | '''Propiedades Cualitativas en las teorías de Green y Naghdi de la Termoelasticidad''' | + | '''Propiedades Cualitativas en las teorías de Green y Naghdi de la |
| | + | Termoelasticidad''' |
| | | | |
| - | '''Resumen:''' En esta presentación recordamos las ecuaciones que gobiernan las teorías de la termoelasticidad de Green y Naghdi. Estas teorías son tres que sus autores denominaron de tipo I, II y III respectivamente. La más general de ellas es la de tipo III que contiene las de tipo I y II como casos límite. | + | '''Resumen:''' En esta presentación recordamos las ecuaciones que |
| | + | gobiernan las teorías de la termoelasticidad de Green y Naghdi. Estas |
| | + | teorías son tres que sus autores denominaron de tipo I, II y III |
| | + | respectivamente. La más general de ellas es la de tipo III que |
| | + | contiene las de tipo I y II como casos límite. |
| | | | |
| - | Nuestro objetivo es hacer un recordatorio de algunas propiedades básicas que satisfacen las soluciones de los sistemas de ecuaciones que determinan estos problemas. Recordaremos diferentes resultados de: | + | Nuestro objetivo es hacer un recordatorio de algunas propiedades |
| | + | básicas que satisfacen las soluciones de los sistemas de ecuaciones |
| | + | que determinan estos problemas. Recordaremos diferentes resultados de: |
| | | | |
| | # Existencia de soluciones | | # Existencia de soluciones |
| Línea 87: |
Línea 168: |
| | (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) | | (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) |
| | | | |
| - | | + | == (Viernes 29-V-2009) Francisco Romero, UCM == |
| - | == Viernes 29-V-2009 de 13:00 a 14:00 Francisco Romero, UCM == | + | |
| | | | |
| | '''Atractores con número de rotación cero. ''' | | '''Atractores con número de rotación cero. ''' |
| | | | |
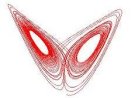
| - | '''Abstract:''' Rotation numbers can be assigned to attractors in two dimensions. We analyzes ome properties of attractors with zero rotation number. The idea of associating a rotation number to an attractor has its origin in the work by Birkhoff and was fully developed by Cartwright and Littlewood. More recently Alligood and Yorke have used these ideas to explore fractal boundaries. Our approach has many points in common with them. but our goal is somehow different. We place the emphasis on results about global attraction and their applicability to differential equations. To be more precise, we consider an orientation-preserving homeomorphism of the plane, denoted by h, and a fixed point <math>p = h(p)</math> that is asymptotically stable. The region of attraction, U, is an open and simply connected subset of <math>R^2</math>. While this implies that U is homeomorphic to the open unit disc the boundary of U can have a complicated structure. | + | '''Abstract:''' Rotation numbers can be assigned to attractors in two |
| | + | dimensions. We analyzes ome properties of attractors with zero |
| | + | rotation number. The idea of associating a rotation number to an |
| | + | attractor has its origin in the work by Birkhoff and was fully |
| | + | developed by Cartwright and Littlewood. More recently Alligood and |
| | + | Yorke have used these ideas to explore fractal boundaries. Our |
| | + | approach has many points in common with them. but our goal is somehow |
| | + | different. We place the emphasis on results about global attraction |
| | + | and their applicability to differential equations. To be more precise, |
| | + | we consider an orientation-preserving homeomorphism of the plane, |
| | + | denoted by h, and a fixed point <math>p = h(p)</math> that is |
| | + | asymptotically stable. The region of attraction, U, is an open and |
| | + | simply connected subset of <math>R^2</math>. While this implies that U |
| | + | is homeomorphic to the open unit disc the boundary of U can have a |
| | + | complicated structure. |
| | | | |
| - | Assuming that U is not <math>R^2</math>, Caratheodory's theory of prime ends associates a copy of the circle S1 to the boundary of U and the map h induces an orientation-preserving homeomorphism of <math>S^1</math>. The corresponding rotation number will be denoted by <math>r = r(h;U)</math>. | + | Assuming that U is not <math>R^2</math>, Caratheodory's theory of |
| | + | prime ends associates a copy of the circle S1 to the boundary of U and |
| | + | the map h induces an orientation-preserving homeomorphism of |
| | + | <math>S^1</math>. The corresponding rotation number will be denoted |
| | + | by <math>r = r(h;U)</math>. |
| | | | |
| - | Our main result says that if <math>r = 0</math>, h is dissipative and U is unbounded then there exists a fixed point in <math>R^2 \backslash U</math>. As a corollary one obtains a criterion for global attraction when p is the unique xed point. The assumption on the unboundedness of the region of attraction is satisfied as soon as h is area-contracting. These are typical assumptions motivated by the theory of nonlinear oscillations. | + | Our main result says that if <math>r = 0</math>, h is dissipative and |
| | + | U is unbounded then there exists a fixed point in <math>R^2 |
| | + | \backslash U</math>. As a corollary one obtains a criterion for global |
| | + | attraction when p is the unique xed point. The assumption on the |
| | + | unboundedness of the region of attraction is satisfied as soon as h is |
| | + | area-contracting. These are typical assumptions motivated by the |
| | + | theory of nonlinear oscillations. |
| | | | |
| - | For maps h coming from differential equations it is not easy to determine the rotation number. This fact was pointed out by Cartwright and Littlewood when they were dealing with the forced Van der Pol equation. In order to make our result applicable we obtain some criteria for the computation of the rotation number. From here we derive consequences for orientation-reversing maps, extinction in population dynamics or global attraction in nonlinear oscillators. | + | For maps h coming from differential equations it is not easy to |
| | + | determine the rotation number. This fact was pointed out by Cartwright |
| | + | and Littlewood when they were dealing with the forced Van der Pol |
| | + | equation. In order to make our result applicable we obtain some |
| | + | criteria for the computation of the rotation number. From here we |
| | + | derive consequences for orientation-reversing maps, extinction in |
| | + | population dynamics or global attraction in nonlinear oscillators. |
| | | | |
| | Viernes 29 de mayo de 13:00 a 14:00, Aula QB63 | | Viernes 29 de mayo de 13:00 a 14:00, Aula QB63 |
| Línea 104: |
Línea 214: |
| | (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) | | (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) |
| | | | |
| - | ==Martes 2-VI-2009 Peter Kloeden (Institute fur Mathematik, JWG, Frankfurt am Main)== | + | == (Viernes 5-VI-2009) Jorge Viveros, Universidad de Méjico== |
| - | | + | |
| - | '''"Random attractors and the preservation of synchronization in the presence of noise" '''
| + | |
| - | | + | |
| - | '''Abstract:''' If two ordinary differential equations with globally asymptotically stable steady state solutions are dissipatively coupled, then the coupled system has a globally asymptotically stable steady state solution which is the cartesion product of the globally asymptotically stable steady state solution of the averaged ordinary differential equation. This property is preserved if the systems are perturbed by additive noise, provided stochastic stationary solutions are used instead of steady state solutions. The formulation and proof require stochastic differentiql equations and ideas from the theory of random dynamical systems. It will be shown that the synchronization effect is also preserved under the discretization of the systems. Synchronization is also possible modulo factorization by the noise for systems with multiplicative noise. This synchronization effect also occurs in reaction diffusion equations on thin domains on either side of a permeable membrane and is preserved in the presence of additve noise.
| + | |
| - | | + | |
| - | | + | |
| - | Martes 2 de junio de 11:00 a 12:00, Aula 209
| + | |
| - | | + | |
| - | (Seminario del Departamento de Matemática Aplicada, Facultad de Ciencias Matemáticas, UCM)
| + | |
| - | | + | |
| - | | + | |
| - | ==Viernes 5-VI-2009 Jorge Viveros, Universidad de Méjico==
| + | |
| | | | |
| | '''"Breathers" en mallas unidimensionales infinitas. ''' | | '''"Breathers" en mallas unidimensionales infinitas. ''' |
| | | | |
| - | '''Resumen:''' El objeto de esta plática es el de introducir tres técnicas muy distintas empleadas para determinar la existencia y en algunos casos también la estabilidad lineal de un tipo especial de soluciones de las ecuaciones de Hamilton para un sistema infinito dimensional con acoplamiento. El tipo de soluciones que nos interesa recibe el nombre de "breathers" y se caracteriza, básicamente, por dos propiedades fundamentales: (quasi-) periodicidad y localización espacial (decaimiento exponencial). Las tres técnicas a presentar son: métodos de continuación (MacKay y Aubry, 1994), teoría de variedad centro (James y Sire, 2004) y teoria KAM (Yuan 2002; Geng, Yi y Viveros, 2008). Cada una de estas técnicas podría ser el objeto de una plática en si, aquí solo nos interesará presentar las ideas básicas, incluyendo los retos que cada uno de los grupos (no exahustivo) de autores arriba mencionados resolvió, así como las preguntas que dejaron abiertas, algunas de las cuales podrían ser el tema de otra charla. | + | '''Resumen:''' El objeto de esta plática es el de introducir tres |
| | + | técnicas muy distintas empleadas para determinar la existencia y en |
| | + | algunos casos también la estabilidad lineal de un tipo especial de |
| | + | soluciones de las ecuaciones de Hamilton para un sistema infinito |
| | + | dimensional con acoplamiento. El tipo de soluciones que nos interesa |
| | + | recibe el nombre de "breathers" y se caracteriza, básicamente, por dos |
| | + | propiedades fundamentales: (quasi-) periodicidad y localización |
| | + | espacial (decaimiento exponencial). Las tres técnicas a presentar |
| | + | son: métodos de continuación (MacKay y Aubry, 1994), teoría de |
| | + | variedad centro (James y Sire, 2004) y teoria KAM (Yuan 2002; Geng, Yi |
| | + | y Viveros, 2008). Cada una de estas técnicas podría ser el objeto de |
| | + | una plática en si, aquí solo nos interesará presentar las ideas |
| | + | básicas, incluyendo los retos que cada uno de los grupos (no |
| | + | exahustivo) de autores arriba mencionados resolvió, así como las |
| | + | preguntas que dejaron abiertas, algunas de las cuales podrían ser el |
| | + | tema de otra charla. |
| | | | |
| | | | |
| Línea 127: |
Línea 240: |
| | (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) | | (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) |
| | | | |
| | + | == (Miércoles 17-VI-2009) Jorge Viveros, Universidad de Méjico== |
| | | | |
| - | ==Miércoles 17-VI-2009 Jorge Viveros, Universidad de Méjico==
| + | '''Continuación de: "Breathers" en mallas unidimensionales infinitas. |
| - | | + | ''' |
| - | '''Continuación de: "Breathers" en mallas unidimensionales infinitas. ''' | + | |
| | | | |
| | | | |
| | (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) | | (planta 6 del pabellón B, Facultad de Ciencias Químicas, UCM) |
| | Jorge Viveros, Universidad de Méjico | | Jorge Viveros, Universidad de Méjico |
Jueves 2 de abril 2009, 12:00-13:00, Aula QC22, (planta 2 del
pabellón C (aulario), Facultad de Ciencias Químicas, UCM)
Viernes 17 de abril, 13:00-14:00, Aula QB63 (planta 6 del
pabellón B, Facultad de Ciencias Químicas, UCM)
== (Viernes 24-IV-2009) José M. Mazón Ruiz, Departamento de Análisis
Matemático, Univ Valencia ==
Viernes 24 de abril, 13:00-14:00, Aula QB63 (planta 6 del pabellón
B, Facultad de Ciencias Químicas, UCM)
== (Jueves 30-IV-2009) Angela Jiménez Casas, Universidad Pontificia
Comillas de Madrid==
Finally we consider a general enthalpy function which allows to study
more general couplings between a diffusion field and a phase-field.
For instance, the phase field can be seen as the density of bacterial
collony or the mass of growing tumor. Analogously, the diffusion field
can stand for the density of nutrient. In this case we prove also the
existence of the metastable solutions of the generalized system.
Material_adicional
Jueves 30 de abril, 13:00-14:00, Aula QB63 (planta 6 del
pabellón B, Facultad de Ciencias Químicas, UCM)
[1] A. Jiménez-Casas, A. Rodriguez-Bernal, Linear stabilility analysis
and metastable solutions for a phase-field model, Proceeding of the
Royal Society of Edimburgh, 129A,571- 600, (1999).
[1] Cioranescu, D. and Saint J. Paulin, J; Homogenization of
Reticulated Structures, Springer
Verlag (1980).
[2] L. Tartar; Probl`emmes d’homogénéisation dans les équations aux
dérivées partielles, Cours
Peccot, Coll`ege de France (1977).
[3] L. Tartar; Quelques remarques sur l´homegénéisation, Function
Analysis and Numerical
Analysis, Proc. Japan-France Seminar 1976, ed. H. Fujita, Japanese
Society for the Promotion
of Science, 468-482 (1978).
Jueves 14 de mayo, 12:00-13:00, Aula QB63 (planta 6 del pabellón
B, Facultad de Ciencias Químicas, UCM)
Nuestro objetivo es hacer un recordatorio de algunas propiedades
básicas que satisfacen las soluciones de los sistemas de ecuaciones
que determinan estos problemas. Recordaremos diferentes resultados de:
For maps h coming from differential equations it is not easy to
determine the rotation number. This fact was pointed out by Cartwright
and Littlewood when they were dealing with the forced Van der Pol
equation. In order to make our result applicable we obtain some
criteria for the computation of the rotation number. From here we
derive consequences for orientation-reversing maps, extinction in
population dynamics or global attraction in nonlinear oscillators.

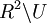 . As a corollary one obtains a criterion for global
attraction when p is the unique xed point. The assumption on the
unboundedness of the region of attraction is satisfied as soon as h is
area-contracting. These are typical assumptions motivated by the
theory of nonlinear oscillations.
. As a corollary one obtains a criterion for global
attraction when p is the unique xed point. The assumption on the
unboundedness of the region of attraction is satisfied as soon as h is
area-contracting. These are typical assumptions motivated by the
theory of nonlinear oscillations.