De Cadedif
(Diferencias entre revisiones)
|
|
| Línea 56: |
Línea 56: |
| | Silesia (Katowice), Polonia nonlinearities" ''' | | Silesia (Katowice), Polonia nonlinearities" ''' |
| | | | |
| - | Jan | + | Jan Cholewa, U. Silesia (Katowice), Polonia |
| | | | |
| | A class of the second order in time semilinear partial differential | | A class of the second order in time semilinear partial differential |
| Línea 64: |
Línea 64: |
| | nonlinear term satisfies certain critical growth conditions. | | nonlinear term satisfies certain critical growth conditions. |
| | | | |
| - | "Dynamical approach to elliptic BVP in asymptotically symmetric | + | '''"Dynamical approach to elliptic BVP in asymptotically symmetric unbounded domains", ''' |
| - | unbounded domains", Messoud Efendiev, Technische Universistät München, | + | |
| - | Alemania | + | Messoud Efendiev, Technische Universistät München, Alemania |
| | + | |
| | We consider dynamical approach to the elliptic problem in | | We consider dynamical approach to the elliptic problem in |
| | asymptotically symmetric unbounded domain and study the large-time | | asymptotically symmetric unbounded domain and study the large-time |
| Línea 75: |
Línea 76: |
| | as well as open problem will also be discussed. | | as well as open problem will also be discussed. |
| | | | |
| - | '''"Non simultaneous quenching in a system of heat equations coupled | + | '''"Non simultaneous quenching in a system of heat equations coupled at the boundary", ''' |
| - | at the boundary", ''' | + | |
| | | | |
| | Raul Ferreira, U. Complutense | | Raul Ferreira, U. Complutense |
| | + | |
| | We study the formation of singularities in finite time for solutions | | We study the formation of singularities in finite time for solutions |
| | of the heat equations coupled at the boundary through a nonlinear flux | | of the heat equations coupled at the boundary through a nonlinear flux |
Revisión de 10:35 20 nov 2007
Seminario del Departamento: CADEDIF Martes 27 de Noviembre de 2007
Departamento de Matemática Aplicada Universidad Complutense de Madrid
Jornada de Dinámica Infinito Dimensional
Martes 27 de Noviembre de 2007
Lugar: Sala 209,
Seminario del Departamento de Matemática Aplicada
Facultad de Ciencias Matemáticas, UCM
9:30-10:20. "Attractors for Parabolic Problems in dumbbell domains",
German Lozada, Univ. Del Estado de Sao Paulo, Brasil
10:20-11:10. "Semilinear Damped Wave Equations with nonlinearities",
Jan Cholewa, U. Silesia (Katowice), Polonia
11:15-11:45. Café
11:45-12:35. "Dynamical approach to elliptic BVP in asymptotically symmetric unbounded domains",
Messoud Efendiev, Technische Universistät München, Alemania
12:35-13:25. "Non simultaneous quenching in a system of heat equations coupled at the boundary",
Raul Ferreira, U. Complutense
Organiza: Grupo de Investigación CADEDIF de la UCM. Parcialmente
financiado por: Proyecto MTM 2006-08262, "Programa de financiación de
Grupos de Investigación UCM-Comunidad de Madrid GR69/06-920894" y
Departamento de Matemática Aplicada, UCM Más información: José M.
Arrieta arrieta@mat.ucm.es Anibal Rodriguez Bernal arober@mat.ucm.es
ABSTRACTS
"Attractors for Parabolic Problems in dumbbell domains"
German Lozada, Univ. del Estado de Sao Paulo, Brasil
In this talk we analyze the dynamics of a parabolic equation with
homogeneous Neumann boundary conditions in the dumbbell domain. We
provide an appropriate functional setting to treat this problem and
show that the attractors behave upper semicontinuous as the channel
shrinks to a line segment.
"Semilinear Damped Wave Equations with fast growing Cholewa, U.
Silesia (Katowice), Polonia nonlinearities"
Jan Cholewa, U. Silesia (Katowice), Polonia
A class of the second order in time semilinear partial differential
equations is considered in the Banach space setting. The results
concerning local existence, regularity, bootstrapping continuation,
and asymptotic properties of solutions are discussed in case when the
nonlinear term satisfies certain critical growth conditions.
"Dynamical approach to elliptic BVP in asymptotically symmetric unbounded domains",
Messoud Efendiev, Technische Universistät München, Alemania
We consider dynamical approach to the elliptic problem in
asymptotically symmetric unbounded domain and study the large-time
behaviour of solutions. Due to the lack of the uniqueness of the
solutions the standard approach based both on the semigroup theory and
on elliptic machinery fails. Our approach based on the trajectory
dynamical systems. Symmetrization and stabilization of the solitions
as well as open problem will also be discussed.
"Non simultaneous quenching in a system of heat equations coupled at the boundary",
Raul Ferreira, U. Complutense
We study the formation of singularities in finite time for solutions
of the heat equations coupled at the boundary through a nonlinear flux
at one border and zero flux at the other border. We characterize, in
terms of the parameters involved when non-simultaneous quenching may
appear. Moreover, if quenching is non-simultaneous we find the
quenching rate and the quenching set. We also find a possible
continuation after quenching of the solutions. Joint work with A. de
Pablo, Mayte Pérez-Llanos, F. Quirós and J. D. Rossi.
iMdea matemáticas:seminario 29 de noviembre 2007
Dpto. de Matemáticas, sala 520 Facultad de Ciencias -
UAM Ciudad Universitaria de Cantoblanco 28049 Madrid
10:30 · 11:10 Hardy inequalities in twisted waveguides
David KREJ CIRÍK
Department of Theoretical Physics, Nuclear Physics Institute, Academy
of Sciences, Rez, Czech Republic e-mail: krejcirik@ujf.cas.cz
The Dirichlet Laplacian in tubular domains is a simple but remarkably
successful model for the quantum Hamiltonian in mesoscopic waveguide
systems. We make an overview of geometrically induced Hardy-type
inequalities established recently for the Laplacian in twisted tubes,
and mention consequences for the electronic transport. We begin by
recalling the classical Hardy inequality and its relation to
geometric, spectral, stochastic and other properties of the underlying
Euclidean space. After discussing the complexity of the problem when
reformulated for quasi-cylindrical subdomains, we give a proof of the
Hardy inequality due to a twist of three-dimensional tubes of uniform
cross-section and use it to prove certain stability of the spectrum.
We also discuss similar effects induced by curvature of the ambient
space or switch of boundary conditions.
11:10 · 11:50 Existence and continuity of global attractors for a
class of non local evolution equations
Antônio L. PEREIRA
Instituto de Matemática e Estatística-USP
Rua do Matão, 1010, Cidade Universitária, São Paulo-SP,
Brasil e-mail: alpereir@ime.usp.br
In this work we prove the existence of a compact global attractor for
the flow of the equation
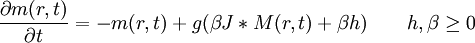
in
L2(S1).
We also show that the flow is gradient and the global attractor
depends continuosly on the parameters h and . AMS subject
classification: 34G20,47H15.
11:50 · 12:10 Coffee break
12:10 · 13:10 Creating materials with desired refraction
coefficient
A. G. RAMM
Mathematics Department, Kansas State University,
Manhattan, KS 66506-2602, USA
ramm@math.ksu.edu
A method is given for calculation of a distribution of small impedance
particles, which should be embedded in a bounded domain, filled with
material with known refraction coefficient, in order that the
resulting new material would have a desired refraction coefficient.
The new material may be created so that it has some desired
wave-focusing properies. For example, it can scatter plane wave mostly
in a fixed solid angle. The inverse scattering problem with scattering
data given at a fixed wave number and at a fixed incident direction is
formulated and solved.
iMdea