De Cadedif
(Diferencias entre revisiones)
|
|
| Línea 3: |
Línea 3: |
| | | | |
| | <center> | | <center> |
| - | Dpto. de Matemáticas, sala 520 Facultad de Ciencias - UAM Ciudad | + | Dpto. de Matemáticas, sala 520 Facultad de Ciencias - |
| - | Universitaria de Cantoblanco 28049 Madrid | + | |
| | + | UAM Ciudad Universitaria de Cantoblanco 28049 Madrid |
| | </center> | | </center> |
| | | | |
| Línea 12: |
Línea 13: |
| | | | |
| | David KREJ CIRÍK | | David KREJ CIRÍK |
| | + | |
| | Department of Theoretical Physics, Nuclear Physics Institute, Academy | | Department of Theoretical Physics, Nuclear Physics Institute, Academy |
| | + | |
| | of Sciences, Rez, Czech Republic e-mail: krejcirik@ujf.cas.cz | | of Sciences, Rez, Czech Republic e-mail: krejcirik@ujf.cas.cz |
| | </center> | | </center> |
| Línea 31: |
Línea 34: |
| | space or switch of boundary conditions. | | space or switch of boundary conditions. |
| | | | |
| - | '''11:10 · 11:50 Existence and continuity of global attractors for a class of non local evolution equations ''' | + | '''11:10 · 11:50 Existence and continuity of global attractors for a |
| | + | class of non local evolution equations ''' |
| | | | |
| | <center> | | <center> |
| | Antônio L. PEREIRA | | Antônio L. PEREIRA |
| | + | |
| | Instituto de Matemática e Estatística-USP | | Instituto de Matemática e Estatística-USP |
| | + | |
| | Rua do Matão, 1010, Cidade Universitária, São Paulo-SP, | | Rua do Matão, 1010, Cidade Universitária, São Paulo-SP, |
| | + | |
| | Brasil e-mail: alpereir@ime.usp.br | | Brasil e-mail: alpereir@ime.usp.br |
| | </center> | | </center> |
| Línea 59: |
Línea 66: |
| | | | |
| | | | |
| - | '''12:10 · 13:10 Creating materials with desired refraction coefficient''' | + | '''12:10 · 13:10 Creating materials with desired refraction |
| | + | coefficient''' |
| | <center> | | <center> |
| | A. G. RAMM | | A. G. RAMM |
| | + | |
| | Mathematics Department, Kansas State University, | | Mathematics Department, Kansas State University, |
| | + | |
| | Manhattan, KS 66506-2602, USA | | Manhattan, KS 66506-2602, USA |
| | + | |
| | ramm@math.ksu.edu | | ramm@math.ksu.edu |
| | </center> | | </center> |
Revisión de 10:15 20 nov 2007
iMdea matemáticas:seminario 29 de noviembre 2007
Dpto. de Matemáticas, sala 520 Facultad de Ciencias -
UAM Ciudad Universitaria de Cantoblanco 28049 Madrid
10:30 · 11:10 Hardy inequalities in twisted waveguides
David KREJ CIRÍK
Department of Theoretical Physics, Nuclear Physics Institute, Academy
of Sciences, Rez, Czech Republic e-mail: krejcirik@ujf.cas.cz
The Dirichlet Laplacian in tubular domains is a simple but remarkably
successful model for the quantum Hamiltonian in mesoscopic waveguide
systems. We make an overview of geometrically induced Hardy-type
inequalities established recently for the Laplacian in twisted tubes,
and mention consequences for the electronic transport. We begin by
recalling the classical Hardy inequality and its relation to
geometric, spectral, stochastic and other properties of the underlying
Euclidean space. After discussing the complexity of the problem when
reformulated for quasi-cylindrical subdomains, we give a proof of the
Hardy inequality due to a twist of three-dimensional tubes of uniform
cross-section and use it to prove certain stability of the spectrum.
We also discuss similar effects induced by curvature of the ambient
space or switch of boundary conditions.
11:10 · 11:50 Existence and continuity of global attractors for a
class of non local evolution equations
Antônio L. PEREIRA
Instituto de Matemática e Estatística-USP
Rua do Matão, 1010, Cidade Universitária, São Paulo-SP,
Brasil e-mail: alpereir@ime.usp.br
In this work we prove the existence of a compact global attractor for
the flow of the equation
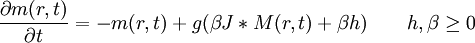
in
L2(S1).
We also show that the flow is gradient and the global attractor
depends continuosly on the parameters h and . AMS subject
classification: 34G20,47H15.
11:50 · 12:10 Coffee break
12:10 · 13:10 Creating materials with desired refraction
coefficient
A. G. RAMM
Mathematics Department, Kansas State University,
Manhattan, KS 66506-2602, USA
ramm@math.ksu.edu
A method is given for calculation of a distribution of small impedance
particles, which should be embedded in a bounded domain, filled with
material with known refraction coefficient, in order that the
resulting new material would have a desired refraction coefficient.
The new material may be created so that it has some desired
wave-focusing properies. For example, it can scatter plane wave mostly
in a fixed solid angle. The inverse scattering problem with scattering
data given at a fixed wave number and at a fixed incident direction is
formulated and solved.
iMdea