December 26, 2024, Thursday, 360

Workshops

De Cadedif

(Diferencias entre revisiones)
(iMdea)
Línea 1: Línea 1:
-
==iMdea matemáticas ==
+
==iMdea matemáticas:seminario  29 de noviembre 2007 ==
-
<center>seminario 
+
<center>
-
29 de noviembre 2007
+
Dpto. de Matemáticas, sala 520 Facultad de Ciencias - UAM Ciudad
-
Dpto. de Matemáticas, sala 520 Facultad de Ciencias - UAM Ciudad Universitaria de Cantoblanco 28049 Madrid
+
Universitaria de Cantoblanco 28049 Madrid
</center>
</center>
-
===10:30 · 11:10 Hardy inequalities in twisted waveguides===
+
'''10:30 · 11:10 Hardy inequalities in twisted waveguides'''
<center>
<center>
 +
David KREJ CIRÍK
David KREJ CIRÍK
-
Department of Theoretical Physics, Nuclear Physics Institute,  Academy of Sciences, Rez, Czech Republic e-mail: krejcirik@ujf.cas.cz
+
Department of Theoretical Physics, Nuclear Physics Institute,  Academy
 +
of Sciences, Rez, Czech Republic e-mail: krejcirik@ujf.cas.cz
</center>
</center>
-
The Dirichlet Laplacian in tubular domains is a simple but remarkably successful model for the quantum Hamiltonian in mesoscopic waveguide systems. We make an overview of geometrically induced Hardy-type inequalities established recently for the Laplacian in twisted tubes, and mention consequences for the electronic transport. We begin by recalling the classical Hardy inequality and its relation to geometric, spectral, stochastic and other properties of the underlying Euclidean space. After discussing the complexity of the problem when reformulated for quasi-cylindrical subdomains, we give a proof of the Hardy inequality due to a twist of three-dimensional tubes of uniform cross-section and use it to prove certain stability of the spectrum. We also discuss similar effects induced by curvature of the ambient space or switch of boundary conditions.
+
The Dirichlet Laplacian in tubular domains is a simple but remarkably
 +
successful model for the quantum Hamiltonian in mesoscopic waveguide
 +
systems. We make an overview of geometrically induced Hardy-type
 +
inequalities established recently for the Laplacian in twisted tubes,
 +
and mention consequences for the electronic transport. We begin by
 +
recalling the classical Hardy inequality and its relation to
 +
geometric, spectral, stochastic and other properties of the underlying
 +
Euclidean space. After discussing the complexity of the problem when
 +
reformulated for quasi-cylindrical subdomains, we give a proof of the
 +
Hardy inequality due to a twist of three-dimensional tubes of uniform
 +
cross-section and use it to prove certain stability of the spectrum.
 +
We also discuss similar effects induced by curvature of the ambient
 +
space or switch of boundary conditions.
-
== 11:10 · 11:50 Existence and continuity of global attractors for a class of non local evolution equations ==
+
'''11:10 · 11:50 Existence and continuity of global attractors for a class of non local evolution equations   '''
<center>
<center>
Línea 25: Línea 39:
Brasil  e-mail: alpereir@ime.usp.br
Brasil  e-mail: alpereir@ime.usp.br
</center>
</center>
-
In this work we prove the existence of a compact global attractor for the flow of the equation
+
In this work we prove the existence of a compact global attractor for
 +
the flow of the equation
<center>
<center>
<math>
<math>
-
\frac{\partial m(r,t)}{\partial t} = -m(r,t)+g(\beta J*M(r,t)+\beta h) \qquad h, \beta \geq 0  
+
\frac{\partial m(r,t)}{\partial t} = -m(r,t)+g(\beta J*M(r,t)+\beta h)
 +
\qquad h, \beta \geq 0  
</math>
</math>
</center>
</center>
Línea 36: Línea 52:
L^{2}(S^{1}).  
L^{2}(S^{1}).  
</math>
</math>
-
We also show that the flow is gradient and the global attractor depends continuosly on the parameters h and . AMS subject classification: 34G20,47H15.
+
We also show that the flow is gradient and the global attractor
 +
depends continuosly on the parameters h and . AMS subject
 +
classification: 34G20,47H15.
-
== 11:50 · 12:10 Coffee break   ==
+
'''11:50 · 12:10 Coffee break '''
-
== 12:10 · 13:10 Creating materials with desired refraction coefficient ==
+
'''12:10 · 13:10 Creating materials with desired refraction coefficient'''
<center>
<center>
A. G. RAMM
A. G. RAMM
Línea 49: Línea 67:
</center>
</center>
-
A method is given for calculation of a distribution of small impedance particles, which should be embedded in a bounded domain, filled with material with known refraction coefficient, in order that the resulting new material would have a desired refraction coefficient. The new material may be created so that it has some desired wave-focusing properies. For example, it can scatter plane wave mostly in a fixed solid angle. The inverse scattering problem with scattering data given at a fixed wave number and at a fixed incident direction is formulated and solved.
+
A method is given for calculation of a distribution of small impedance
 +
particles, which should be embedded in a bounded domain, filled with
 +
material with known refraction coefficient, in order that the
 +
resulting new material would have a desired refraction coefficient.
 +
The new material may be created so that it has some desired
 +
wave-focusing properies. For example, it can scatter plane wave mostly
 +
in a fixed solid angle. The inverse scattering problem with scattering
 +
data given at a fixed wave number and at a fixed incident direction is
 +
formulated and solved.
[http://www.imdea.org iMdea]
[http://www.imdea.org iMdea]

Revisión de 10:14 20 nov 2007

iMdea matemáticas:seminario 29 de noviembre 2007

Dpto. de Matemáticas, sala 520 Facultad de Ciencias - UAM Ciudad Universitaria de Cantoblanco 28049 Madrid


10:30 · 11:10 Hardy inequalities in twisted waveguides

David KREJ CIRÍK Department of Theoretical Physics, Nuclear Physics Institute, Academy of Sciences, Rez, Czech Republic e-mail: krejcirik@ujf.cas.cz


The Dirichlet Laplacian in tubular domains is a simple but remarkably successful model for the quantum Hamiltonian in mesoscopic waveguide systems. We make an overview of geometrically induced Hardy-type inequalities established recently for the Laplacian in twisted tubes, and mention consequences for the electronic transport. We begin by recalling the classical Hardy inequality and its relation to geometric, spectral, stochastic and other properties of the underlying Euclidean space. After discussing the complexity of the problem when reformulated for quasi-cylindrical subdomains, we give a proof of the Hardy inequality due to a twist of three-dimensional tubes of uniform cross-section and use it to prove certain stability of the spectrum. We also discuss similar effects induced by curvature of the ambient space or switch of boundary conditions.

11:10 · 11:50 Existence and continuity of global attractors for a class of non local evolution equations

Antônio L. PEREIRA Instituto de Matemática e Estatística-USP Rua do Matão, 1010, Cidade Universitária, São Paulo-SP, Brasil e-mail: alpereir@ime.usp.br

In this work we prove the existence of a compact global attractor for the flow of the equation

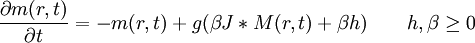
\frac{\partial m(r,t)}{\partial t} = -m(r,t)+g(\beta J*M(r,t)+\beta h) \qquad h, \beta \geq 0

in L2(S1). We also show that the flow is gradient and the global attractor depends continuosly on the parameters h and . AMS subject classification: 34G20,47H15.

11:50 · 12:10 Coffee break


12:10 · 13:10 Creating materials with desired refraction coefficient

A. G. RAMM Mathematics Department, Kansas State University, Manhattan, KS 66506-2602, USA ramm@math.ksu.edu

A method is given for calculation of a distribution of small impedance particles, which should be embedded in a bounded domain, filled with material with known refraction coefficient, in order that the resulting new material would have a desired refraction coefficient. The new material may be created so that it has some desired wave-focusing properies. For example, it can scatter plane wave mostly in a fixed solid angle. The inverse scattering problem with scattering data given at a fixed wave number and at a fixed incident direction is formulated and solved.

iMdea

Obtenido de "http://euler.quim.ucm.es/wiki/index.php/Workshops"