|
|
| (17 ediciones intermedias no se muestran.) |
| Línea 1: |
Línea 1: |
| | __TOC__ | | __TOC__ |
| | | | |
| - | == Carlos Castro (UPM), "Implementación numérica de leyes de | + | == Carlos Castro, UPM, "Implementación numérica de leyes de conservación escalares", 17-I-2008 == |
| - | conservación escalares", 17-I-2008 de 12:30--13:30 == | + | |
| | | | |
| - | Resumen: En esta presentación daremos un repaso general de los métodos | + | Resumen: En esta presentación daremos un repaso general de los métodos numéricos habituales para aproximar soluciones de leyes de conservación escalares. Analizaremos también su implementación práctica y veremos ejemplos en una y dos dimensiones. [[Material_adicional]] |
| - | numéricos habituales para aproximar soluciones de leyes de | + | |
| - | conservación escalares. Analizaremos también su implementación | + | |
| - | práctica y veremos ejemplos en una y dos | + | |
| - | dimensiones.[[Material_adicional]] | + | |
| | | | |
| | ==Mayte Pérez-Llanos, UC3M, "Tres Problemas con Blow-Up", 24-I-2008 == | | ==Mayte Pérez-Llanos, UC3M, "Tres Problemas con Blow-Up", 24-I-2008 == |
| | | | |
| | | | |
| - | '''Resumen: ''' Presentaremos diversos trabajos que tienen como nexo
| + | Resumen: Presentaremos diversos trabajos que tienen como nexo común el análisis del fenómeno de explosión en ciertos problemas de evolución de tipo parabólico. |
| - | común el análisis del fenómeno de explosión en ciertos problemas de | + | |
| - | evolución de tipo parabólico. | + | |
| | | | |
| - | Comenzamos proponiendo un método numérico para tratar el problema de | + | Comenzamos proponiendo un método numérico para tratar el problema de Dirichlet asociado a la ecuación del p−laplaciano con una fuente no lineal en un intervalo acotado. Demostramos que las aproximaciones numéricas obtenidas convergen a las soluciones del problema continuo, y que verifican un principio de comparación, además de otras propiedades. Con ellas reproducimos las condiciones de existencia de explosión, tasas y conjuntos de explosión y comportamiento asintótico conocidos para las soluciones del Problema continuo. |
| - | Dirichlet asociado a la ecuación del p−laplaciano con una fuente no | + | |
| - | lineal en un intervalo acotado. Demostramos que las aproximaciones | + | |
| - | numéricas obtenidas convergen a las soluciones del problema continuo, | + | |
| - | y que verifican un principio de comparación, además de otras | + | |
| - | propiedades. Con ellas reproducimos las condiciones de existencia de | + | |
| - | explosión, tasas y conjuntos de explosión y comportamiento asintótico | + | |
| - | conocidos para las soluciones del Problema continuo. | + | |
| | | | |
| - | A continuación estudiamos un problema asociado al operador doblemente | + | A continuación estudiamos un problema asociado al operador doblemente no lineal con condición de contorno de tipo Neumann no lineal en un intervalo acotado. Demostramos existencia local de soluciones de dicho problema, y determinamos los conjuntos y tasas de explosión en función del valor de los exponentes que intervienen. Asimismo, para cierto valor de los mismos, demostramos la convergencia de las soluciones a un perfil estacionario. |
| - | no lineal con condición de contorno de tipo Neumann no lineal en un | + | |
| - | intervalo acotado. Demostramos existencia local de soluciones de dicho | + | |
| - | problema, y determinamos los conjuntos y tasas de explosión en función | + | |
| - | del valor de los exponentes que intervienen. Asimismo, para cierto | + | |
| - | valor de los mismos, demostramos la convergencia de las soluciones a | + | |
| - | un perfil estacionario. | + | |
| | | | |
| - | Finalizamos dando algunos ejemplos de problemas parabólicos en varias | + | Finalizamos dando algunos ejemplos de problemas parabólicos en varias dimensiones espaciales, cuyas soluciones explotan en compactos no triviales, de dimensión arbitrariamente menor que la del espacio ambiente. Para ello deberemos estudiar el soporte de las soluciones de ciertos problemas elípticos. |
| - | dimensiones espaciales, cuyas soluciones explotan en compactos no | + | |
| - | triviales, de dimensión arbitrariamente menor que la del espacio | + | |
| - | ambiente. Para ello deberemos estudiar el soporte de las soluciones de | + | |
| - | ciertos problemas elípticos. | + | |
| | | | |
| - | En colaboración con Raúl Ferreira (U. Complutense de Madrid), Ján Filo | + | En colaboración con Raúl Ferreira (U. Complutense de Madrid), Ján Filo (U. Comenius, Eslovaquia), Arturo de Pablo (U. Carlos III de Madrid) y Julio D. Rossi (U. de Buenos Aires, Argentina) |
| - | (U. Comenius, Eslovaquia), Arturo de Pablo (U. Carlos III de Madrid) y | + | |
| - | Julio D. Rossi (U. de Buenos Aires, Argentina) | + | |
| | | | |
| - | ==Francisco Montero, Departamento de Bioquímica y Biología Molecular | + | ==Francisco Montero, Departamento de Bioquímica y Biología Molecular I, UCM: "Matemáticas y problemas en bioquímica" 28-II-2008== |
| - | I, UCM: "Matemáticas y problemas en bioquímica" 28-II-2008== | + | |
| | | | |
| - | Resumen: Mi intención es pasar revista a tres problemas: dinámica | + | Resumen: Mi intención es pasar revista a tres problemas: dinámica evolutiva y selectiva de sistemas auto-replicativos con error (fundamentalmente ecuaciones diferenciales ordinarias y modelos estocásticos). tiempos de respuesta en sistemas no lineales (deconvoluciones, transformadas de Fourier, etc..,) y análisis estequimétricos de redes metabólicas (álgebra de matrices, espacios vectoriales convexos, etc..). |
| - | evolutiva y selectiva de sistemas auto-replicativos con error | + | |
| - | (fundamentalmente ecuaciones diferenciales ordinarias y modelos | + | |
| - | estocásticos). tiempos de respuesta en sistemas no lineales | + | |
| - | (deconvoluciones, transformadas de Fourier, etc..,) y análisis | + | |
| - | estequimétricos de redes metabólicas (álgebra de matrices, espacios | + | |
| - | vectoriales convexos, etc..). | + | |
| | | | |
| - | ==Ricardo P. Silva Universidade de São Paulo 6-III-2008 13:00-14:00: | + | ==Ricardo P. Silva, Universidade de São Paulo, Parabolic Problems in thin Domains, 6-III-2008 == |
| - | Parabolic Problems in thin Domains ==
| + | |
| | | | |
| - | Ricardo P. Silva, Departamento De Matemática, Instituto De Ciências | + | Ricardo P. Silva, Departamento De Matemática, Instituto De Ciências Matemáticas e de Computação, Universidade de São Paulo-Campus De São Carlos, Caixa Postal 668, 13560- 970 São Carlos Sp, Brazil We study semilinear reaction-diffusion problems of the type <center> <math> u_t(x,t) = \Delta u(x,t)+f(u(x,t)), \Omega \times (0,\infty) </math> </center> <center> <math> \frac{\partial u}{\partial \nu}(x,t) = 0, \partial \Omega \times (0,\infty). </math> </center> |
| - | Matemáticas e de Computação, Universidade de São Paulo-Campus De São | + | |
| - | Carlos, Caixa Postal 668, 13560- 970 São Carlos Sp, Brazil We study | + | |
| - | semilinear reaction-diffusion problems of the type <center> <math> | + | |
| - | u_t(x,t) = \Delta u(x,t)+f(u(x,t)), \Omega \times (0,\infty) | + | |
| - | </math> </center> <center> <math> \frac{\partial u}{\partial \nu}(x,t) | + | |
| - | = 0, \partial \Omega \times (0,\infty). </math> </center> | + | |
| | | | |
| - | We develop a abstract theory to obtain the continuity of the | + | We develop a abstract theory to obtain the continuity of the asymptotic dynamics of <math>(P) </math> under singular perturbations of the spatial domain <math>\Omega </math> and we apply that to many examples in ''thin domains. '' |
| - | asymptotic dynamics of <math>(P) </math> under singular perturbations | + | |
| - | of the spatial domain <math>\Omega </math> and we apply that to many | + | |
| - | examples in ''thin domains. '' | + | |
| | | | |
| | '''Aula QB62 ''' | | '''Aula QB62 ''' |
| | | | |
| - | ==Héctor Tejero, Departamento de Bioquímica y Biología Molecular I, | + | ==Héctor Tejero, Departamento de Bioquímica y Biología Molecular I, UCM, Dinámica de cuasiespecies teóricas: aproximación determinista, 27-III-2008 == |
| - | UCM 27-III-2008 13:00-14:00 Dinámica de cuasiespecies teóricas: | + | |
| - | aproximación determinista == | + | |
| | | | |
| - | '''Resumen:''' El modelo de Eigen trata de explicar mediante el uso de | + | '''Resumen:''' El modelo de Eigen trata de explicar mediante el uso de ecuaciones diferenciales ordinarias la dinámica evolutiva de especies autorreplicantes sometidas a altas tasas de mutación. De este modelo resulta que en estas condiciones las poblaciones son distribuciones de mutantes denominadas cuasiespecies. Dicho modelo también predice un límite máximo para la tasa de mutación que puede soportar una población denominado umbral de error. Finalmente, se planteará en qué condiciones se puede producir la extinción de la población y cual es su relación con el umbral de error' |
| - | ecuaciones diferenciales ordinarias la dinámica evolutiva de especies | + | |
| - | autorreplicantes sometidas a altas tasas de mutación. De este modelo | + | |
| - | resulta que en estas condiciones las poblaciones son distribuciones de | + | |
| - | mutantes denominadas cuasiespecies. Dicho modelo también predice un | + | |
| - | límite máximo para la tasa de mutación que puede soportar una | + | |
| - | población denominado umbral de error. Finalmente, se planteará en qué | + | |
| - | condiciones se puede producir la extinción de la población y cual es | + | |
| - | su relación con el umbral de error' | + | |
| | | | |
| - | '''(Atencion al aula QC11) '''
| + | ==Karina Schiabel-Silva Dep Mat, Univ Federal de Sao Carlos, Brasil, Continuidad de Atractores para Problemas Parabólicos Semilineales con Difusión alta localizada, 3-IV-2008 == |
| | | | |
| - | ==Karina Schiabel-Silva Dep Mat, Ufscar, Brasil: 3-IV-2008 13-14
| |
| - | Continuidad de Atractores para Problemas Parabólicos Semilineales con
| |
| - | Difusión alta localizada ==
| |
| | | | |
| | + | El objetivo es estudiar el comportamiento asintótico de problemas parabólicos semilineales del tipo <center> <math> u_t - div(p(x)\nabla(u))+ \lambda u = f(u) </math> </center> en un dominio limitado e regular <math> \Omega \subset \mathbb{R}^n </math> cuando el coeficiente de difusión <math>p </math> tiende al infinito en una sub-region <math> \Omega_0 </math> interior al dominio físico <math> \Omega_0 </math> Probamos que, sob determinadas hipótesis, la família de atractores es semicontinua inferior y superiormente cuando la difusión explota en <math> \Omega_0 </math>. '''(Atencion al aula QC11) ''' |
| | | | |
| - | El objetivo es estudiar el comportamiento asintótico
| + | == Julio Rossi, IMDEA Matemáticas, Madrid, Ecuaciones de evolución no locales, 10-IV-2008 == |
| - | de problemas parabólicos semilineales del tipo
| + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | u_t - div(p(x)\nabla(u))+ \lambda u = f(u)
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | en un dominio limitado e regular
| + | |
| - | <math>
| + | |
| - | \Omega \subset \mathbb{R}^n
| + | |
| - | </math>
| + | |
| - | cuando el coeficiente de difusión
| + | |
| - | <math>p </math>
| + | |
| - | tiende al infinito en una
| + | |
| - | sub-region
| + | |
| - | <math>
| + | |
| - | \Omega_0
| + | |
| - | </math>
| + | |
| - | interior al dominio físico <math>
| + | |
| - | \Omega_0
| + | |
| - | </math>
| + | |
| - | Probamos que, sob determinadas hipótesis, la família de
| + | |
| - | atractores es semicontinua inferior y superiormente cuando la
| + | |
| - | difusión explota en <math>
| + | |
| - | \Omega_0
| + | |
| - | </math>.
| + | |
| - | '''(Atencion al aula QC11) '''
| + | |
| | | | |
| - | == Julio Rossi, Prof. IMDEA (IMDEA Matemáticas, Madrid, España):
| + | Resumen: Presentaremos una serie de resultados sobre ecuaciones no locales de la forma <center> <math> u_t = J*u - u. </math> </center> |
| - | 10-IV-2008 13-14: Ecuaciones de evolución no locales. ==
| + | |
| | | | |
| - | Resumen:
| |
| - | Presentaremos una serie de resultados sobre ecuaciones no locales de
| |
| - | la forma
| |
| - | <center>
| |
| - | <math>
| |
| - | u_t = J*u - u.
| |
| - | </math>
| |
| - | </center>
| |
| | | | |
| - | '''Aula QC11 '''
| |
| | | | |
| - | ==Fabricio Macia Lang, Departamento de Matemática Aplicada, UCM | + | ==David Usero, Departamento de Matemática Aplicada, UCM, "What if n=1/2?". Modelización a través del Cálculo Fraccionario, 8-V-2008 == |
| - | 24-IV-2008 13:--14: Aspectos matemáticos del límite semiclásico de
| + | |
| - | la mecánica cuántica en una variedad compacta. ==
| + | |
| | | | |
| - | Resumen. Describiremos algunos resultados sobre el límite semiclásico
| |
| - | de la mecánica cuántica en una variedad Riemanniana compacta.
| |
| - | Mostraremos como dicho límite viene determinado por el flujo geodésico
| |
| - | de la variedad y cómo el resultado depende de la escala temporal
| |
| - | considerada.
| |
| | | | |
| - | '''Aula QC11 '''
| + | ==Valeri Makarov, Dept. Mat. Apl, UCM Análisis e interpretación de la actividad electroencefalográfica, 22-V-08== |
| | | | |
| - | ==David Usero, Departamento de Matemática Aplicada, UCM, 8-V-2008
| + | Resumen: El procesamiento de información en el cerebro conlleva la actividad de múltiples tipos neuronales organizados funcionalmente en circuitos locales o de largo recorrido. Esta actividad se recoge en el electroencefalograma (EEG), un potencial contribuido por corrientes postsinápticas iniciadas tanto por neuronas locales como extrínsecas. Sólo algunos eventos (neuronales y/o de origen artificial) muy sincronizados en regiones laminadas producen patrones de EEG con amplitud notable. Sin embargo, estos eventos destacados en el EEG constituyen una pequeña fracción de la actividad total y enmascaran contribuciones neuronales importantes pero menos sincrónicas. En esta presentación discutiremos un nuevo procedimiento para estudiar la dinámica de poblaciones neuronales, que permite rescatar la información extraordinariamente rica contenida en un EEG. Esta técnica nos permite descomponer el EEG original en la actividad independiente de varias fuentes o generadores cuyo comportamiento se puede modelar mediante osciladores acoplados. Veremos el posible papel de retardos en la propagación de la señal en un modelo de la red neuronal. |
| - | 15:00-16:00 "What if n=1/2?". Modelización a través del Cálculo
| + | |
| - | Fraccionario.==
| + | |
| | | | |
| - | '''Aula QB63 '''
| |
| | | | |
| - | ==Valeri Makarov, Dept. Mat. Apl, UCM 22-05-08 13:00-14:00: Análisis | + | ==Pier Domenico Lamberti, Università degli Studi di Padova, Italia, On a peculiar 'transition operator', 17-VI-2008 == |
| - | e interpretación de la actividad electroencefalográfica==
| + | |
| | | | |
| - | Resumen: El procesamiento de información en el cerebro conlleva la
| + | ''' Abstract:''' We discuss the proof of inequalities of the type <center> <math> |
| - | actividad de múltiples tipos neuronales organizados funcionalmente en
| + | |\lambda_n[\Omega_1]-\lambda_n[\Omega_2 ]|\le c_n |
| - | circuitos locales o de largo recorrido. Esta actividad se recoge en el
| + | |\Omega_1\vartriangle \Omega_2|, </math> </center> |
| - | electroencefalograma (EEG), un potencial contribuido por corrientes
| + | |
| - | postsinápticas iniciadas tanto por neuronas locales como extrínsecas.
| + | |
| - | Sólo algunos eventos (neuronales y/o de origen artificial) muy
| + | |
| - | sincronizados en regiones laminadas producen patrones de EEG con
| + | |
| - | amplitud notable. Sin embargo, estos eventos destacados en el EEG
| + | |
| - | constituyen una pequeña fracción de la actividad total y enmascaran
| + | |
| - | contribuciones neuronales importantes pero menos sincrónicas.
| + | |
| - | En esta presentación discutiremos un nuevo procedimiento para estudiar
| + | |
| - | la dinámica de poblaciones neuronales, que permite rescatar la
| + | |
| - | información extraordinariamente rica contenida en un EEG. Esta técnica
| + | |
| - | nos permite descomponer el EEG original en la actividad independiente
| + | |
| - | de varias fuentes o generadores cuyo comportamiento se puede modelar
| + | |
| - | mediante osciladores acoplados. Veremos el posible papel de retardos
| + | |
| - | en la propagación de la señal en un modelo de la red neuronal.
| + | |
| | | | |
| - | '''Aula QB63 ''' | + | where <math> \lambda_n[\Omega ] </math>, <math> n\in {\mathbb{N}} </math>, denote the eigenvalues of a second order uniformly elliptic operator on a domain <math> \Omega </math> in <math> {\mathbb{R}}^N </math> and <math>|\Omega_1\vartriangle \Omega_2|</math> denotes the Lebesgue measure of the symmetric difference of <math>\Omega_1</math> and <math>\Omega_2</math>. Particular attention is devoted to homogeneous Dirichlet boundary conditions for which a peculiar operator <math>T_{12}:W^{1,2}(\Omega_1 )\to W^{1,2}(\Omega_2 )</math> mapping <math>W^{1,2}_0(\Omega _1)</math> to <math>W^{1,2}_0(\Omega _2)</math> is constructed in order to compare the Rayleigh quotients corresponding to the problems on <math>\Omega_1</math> and <math>\Omega_2</math>. This operator replaces the restriction operator typically used for Neumann boundary conditions and can also be used for Neumann or mixed Dirichlet-Neumann boundary conditions. In the terminology of '''2 ''' <math>T_{12}</math> is a transition operator. The talk is based on the material published in '''1''' |
| | | | |
| - |
| + | '''References ''' |
| | + | #Spectral stability of Dirichlet second order uniformly elliptic operators}, '' J.~Differential Equations'', ''' 244''', pp.~1712-1740, 2008. |
| | + | # V.I.~Burenkov, P.D.~Lamberti, Spectral stability of general non-negative self-adjoint operators with applications to Neumann-type operators., ''J.~Differential Equations'', ''' 233 ''',pp.~345-379, 2007. |
| | | | |
| - | ==Pier Domenico Lamberti, Dip di Mat Pura e Aplicata Università degli
| |
| - | Studi di Padova, Italia, 11-06-08 12:00 Spectral stability estimates
| |
| - | for elliptic operators in domain perturbation problems ==
| |
| | | | |
| - | ''' Abstract:'''
| + | ==Henar Herrero, Univ Castilla La Mancha, Un problema de convección con viscosidad variable, 21-IX-2008 == |
| - | We consider the problem of finding estimates for the variation
| + | |
| - | of the eigenvalues of partial differential operators of elliptic type
| + | |
| - | following
| + | |
| - | a domain perturbation.
| + | |
| - | We survey several results and we present some estimates of the type
| + | |
| - | <center>
| + | |
| - | <math>
| + | |
| - | |\lambda_n[\Omega_1]-\lambda_n[\Omega_2 ]|\le c_n \delta (\Omega_1 ,
| + | |
| - | \Omega_2),\ \ \ \ n\in {\mathbb{N}},
| + | |
| - | </math>
| + | |
| - | </center>
| + | |
| - | for some constant <math> c_n </math> depending on <math> n </math>,
| + | |
| - | where <math>\lambda_n[\Omega _1]</math>, <math>\lambda_n[\Omega
| + | |
| - | _2]</math> denote the eigenvalues of operators defined on the open
| + | |
| - | subsets <math>\Omega_1, \Omega_2</math> of <math>{\mathbb{R}}^N</math>
| + | |
| - | respectively, and <math>\delta (\Omega_1 , \Omega_2)</math> is a
| + | |
| - | convenient `measure of vicinity' of <math>\Omega_1</math>,
| + | |
| - | <math>\Omega_2</math> ({e.g.,} Hausdorff distance, Lebesgue measure of
| + | |
| - | <math>\Omega _1\vartriangle \Omega_2</math>, etc.). Joint work with
| + | |
| - | Victor I. Burenkov.
| + | |
| | | | |
| - | '''Aula 209 ''' | + | '''Resumen:''' Debido a las diferencias de temperatura entre la corteza terrestre y el núcleo externo de la Tierra existe la posibilidad térmica de formación de una corriente convectiva que abarque todo el manto. |
| | | | |
| - | ==Continuación de Valeri Makarov 12-06-08 13:00--14:00 ==
| + | La convección en el manto terrestre es un proceso de dinámica de fluidos que parece determinar el movimiento de las placas tectónicas y, en consecuencia la deriva de los continentes. Existe una tendencia general de aumento de la viscosidad con la profundidad, pero esta relación no es lineal. Acercarnos a un modelo de convección en el manto terrestre es el motivo por el que estudiamos un problema de convección en el que la viscosidad es una función de la temperatura en las ecuaciones de Navier-Stokes. Estudiamos desde un punto de vista teórico y numérico este problema, tanto la existencia y cálculo numérico de soluciones como las distintas bifurcaciones. En el estudio numérico consideramos una dependencia exponencial de la temperatura en la viscosidad. Realizamos un estudio comparativo de bifurcaciones para viscosidad constante y para distintos perfiles de viscosidad variable y realizamos un estudio exhaustivo de bifurcaciones presentado diagramas de equilibrio con viscosidad constante y variable con distintas relaciones de aspecto y considerando zonas de codimensión dos. |
| - | '''Aula QB63'''
| + | |
| | | | |
| | | | |
| - | ==Pier Domenico Lamberti 17-06-2008 13:00--14:00:On a peculiar | + | ==Fabricio Macia Lang, ETSI Navales, UPM, Aspectos matemáticos del límite semiclásico de la mecánica cuántica en una variedad compacta, 24-X-2008 == |
| - | `transition operator' ==
| + | |
| | | | |
| | + | '''Resumen:''' Describiremos algunos resultados sobre el límite semiclásico de la mecánica cuántica en una variedad Riemanniana compacta. Mostraremos como dicho límite viene determinado por el flujo geodésico de la variedad y cómo el resultado depende de la escala temporal considerada. [[Material_adicional]] |
| | | | |
| | + | '''Aula QB62 ''' |
| | + | |
| | | | |
| - | ''' Abstract:''' | + | ==Alexandre N. Carvalho, Univ de São Paulo, Brasil, Asymptotic dynamics under singular perturbations, 31-X-2008 == |
| - | We discuss the proof of inequalities of the type | + | |
| - | <center>
| + | |
| - | <math>
| + | '''Resumen:''' In this lecture we present an overview of several singular perturbation problems. We also present our approach to show that some singular perturbations do not affect in a significant way the asymptotic behavior of such problems. |
| - | |\lambda_n[\Omega_1]-\lambda_n[\Omega_2 ]|\le c_n
| + | |
| - | |\Omega_1\vartriangle \Omega_2|,
| + | Aula QB62, planta 6 del pabellón B |
| - | </math>
| + | |
| - | </center>
| + | == David Pérez García, Dep. Análisis Matemático,UCM, El reto de entender y simular sistemas cuánticos en 2D, Viernes 21-XI-2008, 12:30-13:30, Aula QB62, planta 6 del pabellón B == |
| | | | |
| - | where <math> \lambda_n[\Omega ] </math>, <math> n\in {\mathbb{N}}
| |
| - | </math>, denote the eigenvalues of a second order uniformly elliptic
| |
| - | operator on a domain <math> \Omega </math> in <math> {\mathbb{R}}^N
| |
| - | </math> and <math>|\Omega_1\vartriangle \Omega_2|</math> denotes the
| |
| - | Lebesgue measure of the symmetric difference of <math>\Omega_1</math>
| |
| - | and <math>\Omega_2</math>. Particular attention is devoted to
| |
| - | homogeneous Dirichlet boundary conditions for which a peculiar
| |
| - | operator <math>T_{12}:W^{1,2}(\Omega_1 )\to W^{1,2}(\Omega_2 )</math>
| |
| - | mapping <math>W^{1,2}_0(\Omega _1)</math> to <math>W^{1,2}_0(\Omega
| |
| - | _2)</math> is constructed in order to compare the Rayleigh quotients
| |
| - | corresponding to the problems on <math>\Omega_1</math> and
| |
| - | <math>\Omega_2</math>. This operator replaces the restriction operator
| |
| - | typically used for Neumann boundary conditions and can also be used
| |
| - | for Neumann or mixed Dirichlet-Neumann boundary conditions. In the
| |
| - | terminology of \cite{bulaneu} <math>T_{12}</math> is a transition
| |
| - | operator. The talk is based on the material published in
| |
| - | <ref name="bula" > V.I.~Burenkov, P.D.~Lamberti, {Spectral stability of
| |
| - | Dirichlet second order uniformly elliptic operators}, {\it
| |
| - | J.~Differential Equations}, {\bf 244},
| |
| - | pp.~1712-1740, 2008. </ref>
| |
| - | \cite{bula}.
| |
| | | | |
| | + | == Arturo de Pablo, Universidad Carlos III de Madrid, Coeficientes críticos en problemas de explosión, Viernes 28-XI-2008, 12:30-13:30,Aula QB62, planta 6 del pabellón B == |
| | | | |
| | + | '''Resumen:''' En esta charla presentaremos una panorámica de algunos problemas de explosión desde el punto de vista de los coeficientes involucrados. En particular estaremos interesados en problemas en los que la presencia de dos términos opuestos produce comportamientos muy diversos y en los casos críticos en los que existe un balance nos planteamos el estudio de la influencia de un coeficiente en uno de los términos. |
| | | | |
| | | | |
| - | \bibitem{bula}
| + | == Jan Cholewa, Universidad de Silesia, Katowice, Polonia, Dissipative semigroups in metric spaces, Viernes 5-XII-2008, 12:30-13:30,Aula QB62, planta 6 del pabellón B == |
| | | | |
| - | \bibitem{bulaneu} V.I.~Burenkov, P.D.~Lamberti, {Spectral stability of
| + | '''Resumen:''' Relations between different notions of dissipativeness are exhibited and |
| - | general non-negative self-adjoint operators with applications to
| + | the conditions that lead to the existence of a maximal compact invariant set are |
| - | Neumann-type operators.}, {\it J.~Differential Equations}, {\bf 233},
| + | discussed. Certain notions of asymptotic compactness are also considered, which |
| - | pp.~345-379, 2007.
| + | are suitable to show that point dissipative implies compact dissipative. |
| - | \end{thebibliography}
| + | |
| | | | |
| | + | [1] J. W. Cholewa, J. K. Hale, Some counterexamples in dissipative systems, Dynam. |
| | + | Contin. Discrete Impuls. Systems. 7 (2000), 159-176. |
| | | | |
| - | '''Aula: QB63 '''
| + | [2] J. W. Cholewa, J. K. Hale, From point dissipative to compact dissipative - addendum to Some counterexamples in dissipative systems, Dynam. Contin. Discrete |
| | + | Impuls. Systems 14, 2007, 147-164. |
Resumen: En esta presentación daremos un repaso general de los métodos numéricos habituales para aproximar soluciones de leyes de conservación escalares. Analizaremos también su implementación práctica y veremos ejemplos en una y dos dimensiones. Material_adicional
Resumen: Presentaremos diversos trabajos que tienen como nexo común el análisis del fenómeno de explosión en ciertos problemas de evolución de tipo parabólico.
Comenzamos proponiendo un método numérico para tratar el problema de Dirichlet asociado a la ecuación del p−laplaciano con una fuente no lineal en un intervalo acotado. Demostramos que las aproximaciones numéricas obtenidas convergen a las soluciones del problema continuo, y que verifican un principio de comparación, además de otras propiedades. Con ellas reproducimos las condiciones de existencia de explosión, tasas y conjuntos de explosión y comportamiento asintótico conocidos para las soluciones del Problema continuo.
A continuación estudiamos un problema asociado al operador doblemente no lineal con condición de contorno de tipo Neumann no lineal en un intervalo acotado. Demostramos existencia local de soluciones de dicho problema, y determinamos los conjuntos y tasas de explosión en función del valor de los exponentes que intervienen. Asimismo, para cierto valor de los mismos, demostramos la convergencia de las soluciones a un perfil estacionario.
Finalizamos dando algunos ejemplos de problemas parabólicos en varias dimensiones espaciales, cuyas soluciones explotan en compactos no triviales, de dimensión arbitrariamente menor que la del espacio ambiente. Para ello deberemos estudiar el soporte de las soluciones de ciertos problemas elípticos.
En colaboración con Raúl Ferreira (U. Complutense de Madrid), Ján Filo (U. Comenius, Eslovaquia), Arturo de Pablo (U. Carlos III de Madrid) y Julio D. Rossi (U. de Buenos Aires, Argentina)
Resumen: Mi intención es pasar revista a tres problemas: dinámica evolutiva y selectiva de sistemas auto-replicativos con error (fundamentalmente ecuaciones diferenciales ordinarias y modelos estocásticos). tiempos de respuesta en sistemas no lineales (deconvoluciones, transformadas de Fourier, etc..,) y análisis estequimétricos de redes metabólicas (álgebra de matrices, espacios vectoriales convexos, etc..).
Ricardo P. Silva, Departamento De Matemática, Instituto De Ciências Matemáticas e de Computação, Universidade de São Paulo-Campus De São Carlos, Caixa Postal 668, 13560- 970 São Carlos Sp, Brazil We study semilinear reaction-diffusion problems of the type
We develop a abstract theory to obtain the continuity of the asymptotic dynamics of (P) under singular perturbations of the spatial domain Ω and we apply that to many examples in thin domains.
El objetivo es estudiar el comportamiento asintótico de problemas parabólicos semilineales del tipo
Probamos que, sob determinadas hipótesis, la família de atractores es semicontinua inferior y superiormente cuando la difusión explota en
.
Resumen: Presentaremos una serie de resultados sobre ecuaciones no locales de la forma
Resumen: El procesamiento de información en el cerebro conlleva la actividad de múltiples tipos neuronales organizados funcionalmente en circuitos locales o de largo recorrido. Esta actividad se recoge en el electroencefalograma (EEG), un potencial contribuido por corrientes postsinápticas iniciadas tanto por neuronas locales como extrínsecas. Sólo algunos eventos (neuronales y/o de origen artificial) muy sincronizados en regiones laminadas producen patrones de EEG con amplitud notable. Sin embargo, estos eventos destacados en el EEG constituyen una pequeña fracción de la actividad total y enmascaran contribuciones neuronales importantes pero menos sincrónicas. En esta presentación discutiremos un nuevo procedimiento para estudiar la dinámica de poblaciones neuronales, que permite rescatar la información extraordinariamente rica contenida en un EEG. Esta técnica nos permite descomponer el EEG original en la actividad independiente de varias fuentes o generadores cuyo comportamiento se puede modelar mediante osciladores acoplados. Veremos el posible papel de retardos en la propagación de la señal en un modelo de la red neuronal.
La convección en el manto terrestre es un proceso de dinámica de fluidos que parece determinar el movimiento de las placas tectónicas y, en consecuencia la deriva de los continentes. Existe una tendencia general de aumento de la viscosidad con la profundidad, pero esta relación no es lineal. Acercarnos a un modelo de convección en el manto terrestre es el motivo por el que estudiamos un problema de convección en el que la viscosidad es una función de la temperatura en las ecuaciones de Navier-Stokes. Estudiamos desde un punto de vista teórico y numérico este problema, tanto la existencia y cálculo numérico de soluciones como las distintas bifurcaciones. En el estudio numérico consideramos una dependencia exponencial de la temperatura en la viscosidad. Realizamos un estudio comparativo de bifurcaciones para viscosidad constante y para distintos perfiles de viscosidad variable y realizamos un estudio exhaustivo de bifurcaciones presentado diagramas de equilibrio con viscosidad constante y variable con distintas relaciones de aspecto y considerando zonas de codimensión dos.
[1] J. W. Cholewa, J. K. Hale, Some counterexamples in dissipative systems, Dynam.
Contin. Discrete Impuls. Systems. 7 (2000), 159-176.
[2] J. W. Cholewa, J. K. Hale, From point dissipative to compact dissipative - addendum to Some counterexamples in dissipative systems, Dynam. Contin. Discrete
Impuls. Systems 14, 2007, 147-164.
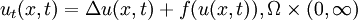

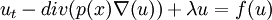
 cuando el coeficiente de difusión p tiende al infinito en una sub-region Ω0 interior al dominio físico Ω0 Probamos que, sob determinadas hipótesis, la família de atractores es semicontinua inferior y superiormente cuando la difusión explota en Ω0. (Atencion al aula QC11)
cuando el coeficiente de difusión p tiende al infinito en una sub-region Ω0 interior al dominio físico Ω0 Probamos que, sob determinadas hipótesis, la família de atractores es semicontinua inferior y superiormente cuando la difusión explota en Ω0. (Atencion al aula QC11)
![|\lambda_n[\Omega_1]-\lambda_n[\Omega_2 ]|\le c_n
|\Omega_1\vartriangle \Omega_2|,](/wiki/images/math/e/0/b/e0bb92d5531b82a98ed603fa8b6bcfca.png)
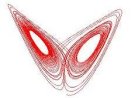

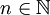 , denote the eigenvalues of a second order uniformly elliptic operator on a domain
, denote the eigenvalues of a second order uniformly elliptic operator on a domain 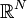 and
and 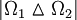 denotes the Lebesgue measure of the symmetric difference of
denotes the Lebesgue measure of the symmetric difference of 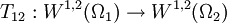 mapping
mapping 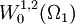 to
to 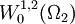 is constructed in order to compare the Rayleigh quotients corresponding to the problems on
is constructed in order to compare the Rayleigh quotients corresponding to the problems on