De Cadedif

Revisión de 13:47 7 mar 2008 (ver código fuente) Cadedif (Discusión | contribuciones) ← Edición más antigua		Última versión de 12:38 27 jun 2022 (ver código fuente) Cadedif (Discusión | contribuciones) (Unified format header)
(9 ediciones intermedias no se muestran.)
Línea 1:		Línea 1:
-	El grupo de investigación viene realizando "Seminarios de caracter	+	= Seminarios Cadedif (Curso 21-22) =
-	informal" desde Octubre del 2006.  Cada semana, un miembro del grupo	+
-	de investigación o bien un investigador invitado externo al grupo	+
-	expone algún tema de investigación de su interés. Las sesiones son	+
-	dinámicas y participativas. Los objetivos de este seminario son:	+
-	* familiarizarnos con los distintos temas de investigación de los	+	El grupo CADEDIF organiza a lo largo del curso un seminario informal del grupo de investigación además de promover Seminarios del Departamento.
-	miembros del grupo.	+
-	* fomentar la interacción científica entre los distintos miembros del	+
-	grupo.	+
-	* establecer posibles vias de cooperación científica tanto entre los	+
-	miembros del grupo como con investigadores externos.	+
-	Seminarios por años.	+	== 23 de Noviembre, Jan Cholewa (U. Silesia, Polonia), ==
-	*[[Seminarios 2006 ]]	+	On exponential and global attractors for lattice and reaction-diffusion type problems
-	*[[Seminarios 2007 ]]	+
-	*[[Seminarios 2006 ]]	+
-	__TOC__	+	== 14 de diciembre, Uwe Brauer (UCM), ==
		+	Global existence of a nonlinear wave equation arising from Nordström's theory of gravitation (joint work with Lavi Karp)
		+	'''Abstract:''' We show global existence of classical solutions for the nonlinear Nordström theory with a source term and a cosmological constant under the assumption that the source term is small in an appropriate norm, while in some cases no smallness assumption on the initial data is required. In this theory, the gravitational field is described by a single scalar function that satisfies a certain semi-linear wave equation. We consider spatial periodic deviation from the background metric, that is why we study the semi-linear wave equation on the three-dimensional torus <math>\mathbb T^3</math> in the Sobolev spaces <math>H^m(\mathbb T^3)</math>. We apply two methods to achieve the existence of global solutions, the first one is by Fourier series, and in the second one, we write the semi-linear wave equation in a non-conventional way as a symmetric hyperbolic system. We also provide results concerning the asymptotic behavior of these solutions and, finally, a blow-up result if the conditions of our global existence theorems are not met.
-	== Alejandro Vidal: Introducción a la teoría de sistemas dinámicos no	+	== 14 de Febrero J. Soria (UCM), ==
-	autónomos. 14-XI-2006 y 18-01-2007 ==	+
-	En primer lugar haremos un muy breve repaso de la teoría de semigrupos	+	Operadores maximales: de los espacios Euclídeos a los grafos de Euler
-	y sistemas dinámicos autónomos. A continuación introduciremos una	+
-	herramienta básica para el estudio de sistemas dinámicos no autónomos:	+
-	los operadores de evolución; así como un nuevo concepto de atracción:	+
-	la atracción en sentido pullback. Por último, introduciremos el	+
-	concepto de "Skew-product flow" para el estudio de sistemas no	+
-	autónomos y aleatorios.	+
-	de 12,30 a 13,30	+	Resumen: Empezando con los resultados clásicos del operador maximal de Hardy-Littlewood en espacios euclídeos:
		+	* acotaciones para diversos tipos de medidas;
		+	* propiedades geométricas;
		+	* aplicaciones a problemas de convergencia de aproximaciones de la identidad o soluciones de EDPs,
		+	* queremos adentrarnos también en algunos avances recientes en contextos discretos, como es el caso de la teoría de grafos.
-	== Raul Ferreira: Formación de singularidades en problemas de	+	== 22 de Febrero Pablo Pedregal (UCLM), Seminario de Depto. ==
-	reacción-difusión. 25-I y 1-II-2007 ==	+
-	Trataremos de ver, medíante ejemplos sencillos, las técnicas básicas	+	Sobre una nueva condición de frontera
-	utilizadas en el estudio del comportamiento de la solución de un	+
-	problema de reacción-difusión cerca del tiempo en el que se produce	+
-	una singularidad.	+
		+	'''Resumen''': Estudiaremos subespacios estrictamente contenidos entre page1imay H<sup>1</sup> El estudio de problemas variacionales sobre tales subespacios conduce a condiciones de frontera especiales entre las clásicas de Dirichlet y Neumann. En concreto, bajo hipótesis apropiadas, se establecerá la existencia de minimizadores y se establecerán las condiciones de optimalidad con especial énfasis en las condiciones óptimas de frontera. La motivación para este estudio procede de los problemas inversos en conductividad en dimensión 3.
-	==Sorin Micu: Problemas de controlabilidad unidimensionales J:	+	== 28 de Febrero Mabel Cuesta (LMPA). Seminario de Depto. ==
-	08-II-2007 ==	+
-	Sorin Micu, Universitatea Craiova, Rumania	+	On a quasilinear elliptic equation with Steklov nonlinear boundary conditions of critical growth (Work in collaboration with Liamidi Leadi)
-	Título: Problemas de controlabilidad unidimensionales	+	== 7 de Marzo 2022. Maya Chhetri (U. Greensboro, USA) Seminario de Depto. ==
-	Se consideran diferentes problemas de controlabilidad y se muestra la	+	Bifurcation and multiplicity results for elliptic problems with subcritical nonlinearity on the boundary. (University of North Carolina Greensboro)
-	relación entre éstos y la teoría de momentos. Usando técnicas de	+
-	funciones enteras y análisis de Fourier no armónico, se resuelven los	+
-	correspondiente problemas de momentos. Tambien se estudíarán	+
-	ecuaciones discretas y se describirán las principales dificultades que	+
-	ellas introducen.	+
		+	'''Abstract:''' We consider an elliptic problem coupled with a nonlinear boundary condition, involving nonlinearity with superlinear and subcritical growth at infinity, with a bifurcation parameter as a factor. We will discuss the number of positive solutions with respect to the bifurcation parameter depending on the behavior of the nonlinearity at infinity and at zero. We will combine the re-scaling argument with degree theory and bifurcation theory to prove results. This talk is based on a joint work with S. Bandyopadhyay, B. B. Delgado, N. Mavinga and R. Pardo.
-	==Ángela Jiménez Casas:Introducción a las ecuaciones diferenciales	+	== 28 de Marzo 2022. Anibal Rodriguez-Bernal (UCM), ==
-	estocásticas de ITO y de STRATONOVICH J: 15-II-2007==	+
		+	Principal eigenvalue, maximum principle and stability for nonlocal diffusion equations in metric measure spaces
		+	'''Resumen:''' Mostramos resultados generales en espacios de medida métricos que garantizan que se cumpla el principio del máximo, débil y fuerte, para problemas lineales no locales estacionarios y de evolución
-	Se introducirán las ecuaciones diferenciales estocásticas a través de	+	== 14 de Junio Joaquin Dominguez de Tena (UCM), ==
-	los dos modelos de integración estocásticas de ITO y de STRATONOVICH	+
-	mostrando la relación entre ambas.	+
-	De hecho el principal objetivo del seminario es intentar establecer	+	La ecuación del calor en un dominio exterior
-	las relaciones entre conceptos y procesos relacionados con las	+
-	ecuaciones diferenciales, como son: Evolución-Probabilidad	+
-	condicionada-Procesos de Markov (Procesos de Weinner). Ruido	+
-	Blanco-Integral de Ito- ... entre otros.	+
		+	'''Resumen:''' Estudiaremos el comportamiento de las soluciones de la ecuación del calor en un dominio exterior, es decir, el complementario de un conjunto compacto en R<sup>N</sup>, el cual denominaremos informalmente &quot;agujero&quot;.
		+	Empezaremos presentando los principales resultados de existencia de acuerdo a la teoría de semigrupos en los espacios funcionales más habituales: L<sup>2</sup>, L<sup>p</sup>, C etc. Estudiaremos el comportamiento asintótico para datos iniciales en Lp, centrándonos en el caso de mayor interés en el cual el dato inicial es integrable. Posteriormente daremos una visión distribucional del problema, donde interpretaremos el &quot;agujero&quot; como una perturbación del problema en todo el espacio. Finalmente, y si queda tiempo, trataremos de &quot;llevar el problema al límite&quot;, considerando datos iniciales que admitirán un crecimiento muy grande en el infinito.
-	==Mihaela Negreanu (UCM) Desigualdades discretas de Ingham 22-II y	+	== 21 de Junio Manuel Villanueva Pesqueira (U. P. Comillas), ==
-	27-II-2007 ==	+
		+	Homogeneización más allá de la periodicidad
-		+	Resumen: A lo largo de los años la teoría de la homogeneización ha sido ampliamente desarrollada para estructuras periódicas. Sin embargo, en ciertas ocasiones las hipótesis clásicas de periodicidad son demasiado restrictivas y surge la necesidad de analizar estructuras más complejas. En particular, en este seminario nos centraremos en la generalización a estructuras con «almost-periodic» heterogeneidades. Mostraremos el método propuesto por S.M. Kozlov en «Averaging differential operators with almost periodic, rapidly oscillating coefficients» y analizaremos las dificultades de adaptarlo a problemas en dominios finos con fronteras oscilantes cuasi-periódicas.
-	La desigualdad de Ingham ha jugado un papel fundamental para la	+
-	demostración de desigualdades de observabilidad en los modelos	+
-	continuos que satisfacen la propiedad de separación spectral uniforme.	+
-	Demostramos una version discreta de esta desigualdad, que permite, en	+
-	particular, obtener resultados de observabilidad uniforme para las	+
-	soluciones filtradas del sistema homogéneo completamente discreto en	+
-	el caso <math> \Delta t<\Delta x </math>. La demostración sigue los	+
-	pasos de la clásica de Ingham y utiliza un resultado de carácter	+
-	técnico de Trefethen donde se estima la diferencia entre la	+
-	transformada discreta y continua de Fourier.	+
-		+
-		+
-		+
-	==Rosa Pardo:Problemas de bifurcación  en perturbación de dominios	+
-	13-III y 20-III-2007==	+
-		+
-	El teorema de Crandall y Rabinowitz determina condiciones suficientes	+
-	para que el conjunto de los ceros de una cierta aplicación en una	+
-	bola, sea topológicamente equivalente (o difeomorfo), al conjunto	+
-	<math>(-1,1)\times \{0\} \cup \{0\}\times (-1,1). </math> Nosotros	+
-	intentaremos desarrollar esas ideas en el marco de los problemas de	+
-	perturbación de dominios.	+
-		+
-	[[Material_adicional]]	+
-		+
-		+
-		+
-		+
-		+
-	==Uwe Brauer Problemas de valor inicial y de frontera libre para el	+
-	sistema Euler--Poisson 27-III, 10-IV y 24-IV-2007 ==	+
-		+
-		+
-		+
-	Se trata el sistema Euler--Poisson, que describe la evolución temporal	+
-	de un fluido perfecto con autogravitación. En la primera parte se da	+
-	una introducción a las ecuaciones, esto incluye: el carácter de las	+
-	ecuaciones, los diferentes problemas que se pueden plantear, como por	+
-	ejemplo un problema de datos iniciales donde la densidad puede tener	+
-	soporte compacto o no, un problema de frontera (libre), etc.; además	+
-	las técnicas que se usan para obtener los resultados, en concreto para	+
-	los sistemas simétricos hiperbólicos. Después se presenta un conjunto	+
-	de resultados conocidos tanto locales (existencia local de soluciones	+
-	clásicas), como globales (existencia global de soluciones clásicas	+
-	para datos iniciales pequeños), además de resultados sobre blow up y	+
-	no existencia global	+
-		+
-		+
-		+
-		+
-	==José M. Arrieta: Dinámica Asintótica y Perturbaciones de Dominio: X	+
-	16-05-2007  ==	+
-		+
-		+
-		+
-		+
-	En esta exposición, se presentarán unos resultados sobre el	+
-	comportamiento de la dinámica asintótica y en particular del atractor,	+
-	de una ecuación cuando ciertas perturbaciones actúan sobre ésta. En	+
-	primer lugar plantearemos el problema de una forma general. En segundo	+
-	lugar, detallaremos los resultados para el caso de una ecuación de	+
-	reacción difusión con condición de contorno Neumann homogénea y una	+
-	perturbación general de dominio. Finalmente mencionaremos otros casos	+
-	relevantes, entre ellos el comportamiento de los puntos de equilibrio	+
-	de una ecuación de reacción difusión con condición de contorno no	+
-	lineal, cuando la frontera es altamente oscilante.	+
-		+
-		+
-	==Germán Lozada: Soluciones estacionarias estables no constantes para	+
-	EDPs de tipo parabólico con difusion alta en dominios tipo dumbbell:	+
-	25-X-07 y 8-XI-07 ==	+
-		+
-	En esta exposición hablaremos de la existencia de soluciones	+
-	estacionarias estables no constantes para EDPs de tipo parabolico.	+
-	Esto lo haremos para el caso de difusion alta en condiciones de	+
-	frontera no lineales.	+
-		+
-		+
-		+
-		+
-		+
-		+
-	==Antônio Luiz Pereira, Instituto de Matemática e Estatística da USP,	+
-	São Paulo, Brasil: A  derivation of Hadamard´s  formula: 4-XII-07	+
-	15,00 a 16,00==	+
-		+
-	In this talk we introduce the formalism of Henry [Perturbation of the	+
-	boundary in boundary value problems] for the computation of various	+
-	quantities related to solutions of B.V.Ps with respecto to variations	+
-	of the domain. We then use the formalism to compute the derivative of	+
-	a (simple) eigenvalue of the Dirichlet Laplacian.	+
-		+
-	'''Aula QB65 '''	+
-		+
-	==Sergio Hoyas Calvo, Departamento de Informática, Universidad de	+
-	Valencia: Simulación numérica de altas prestaciones: 12-XII-07:	+
-	15:00--16:00==	+
-		+
-	En esta charla haremos una visión general de las simulaciones	+
-	numéricas de la forma más amplia posible, desde el hardware hasta la	+
-	presentación final de resultados. Empezaremos por un repaso de las	+
-	arquitecturas más usadas en este momento para el cálculo científico,	+
-	deteniéndonos después en el software y herramientas más usadas por la	+
-	comunidad, así como de los métodos usados para pasar del papel al	+
-	código. Como aplicación de estas técnicas, veremos como se realizó una	+
-	simulación de un canal turbulento en una malla de 1.8e10 puntos, que	+
-	entre otras cosas, sirvió para el chequeo intensivo de MareNostrum, el	+
-	mayor supercomputador europeo.[[Material_adicional]]	+
-		+
-		+
-	==Jorge Alvarez Rodrigo: Existencia de soluciones para EDs Elípticas	+
-	de doble no linealidad variable:  18 XII de 15,00 a 16,00 ==	+
-		+
-		+
-	Partiendo de los principales resultados de trabajos previos, se	+
-	presenta una nueva ED Elíptica que combina los casos conocidos de	+
-	exponentes variables. Se indican las confirmaciones experimentales más	+
-	interesantes sobre el tema. La existencia de soluciones para las	+
-	ecuaciones isotrópicas y anisotrópicas centra la demostración	+
-	principal, y se apunta un esbozo de la unicidad. Se pretende presentar	+
-	una extensión original a desarrollar de la teoría conocida sobre este	+
-	tema.	+
-		+
-	== Carlos Castro (UPM), "Implementación numérica de leyes de	+
-	conservación escalares", 17-I-2008 de 12:30--13:30 ==	+
-		+
-	Resumen: En esta presentación daremos un repaso general de los métodos	+
-	numéricos habituales para aproximar soluciones de leyes de	+
-	conservación escalares. Analizaremos también su implementación	+
-	práctica y veremos ejemplos en una y dos	+
-	dimensiones.[[Material_adicional]]	+
-		+
-	==Mayte Pérez-Llanos, UC3M, "Tres Problemas con Blow-Up", 24-I-2008 ==	+
-		+
-		+
-	'''Resumen: ''' Presentaremos diversos trabajos que tienen como nexo	+
-	común el análisis del fenómeno de explosión en ciertos problemas de	+
-	evolución de tipo parabólico.	+
-		+
-	Comenzamos proponiendo un método numérico para tratar el problema de	+
-	Dirichlet asociado a la ecuación del p−laplaciano con una fuente no	+
-	lineal en un intervalo acotado. Demostramos que las aproximaciones	+
-	numéricas obtenidas convergen a las soluciones del problema continuo,	+
-	y que verifican un principio de comparación, además de otras	+
-	propiedades. Con ellas reproducimos las condiciones de existencia de	+
-	explosión, tasas y conjuntos de explosión y comportamiento asintótico	+
-	conocidos para las soluciones del Problema continuo.	+
-		+
-	A continuación estudiamos un problema asociado al operador doblemente	+
-	no lineal con condición de contorno de tipo Neumann no lineal en un	+
-	intervalo acotado. Demostramos existencia local de soluciones de dicho	+
-	problema, y determinamos los conjuntos y tasas de explosión en función	+
-	del valor de los exponentes que intervienen. Asimismo, para cierto	+
-	valor de los mismos, demostramos la convergencia de las soluciones a	+
-	un perfil estacionario.	+
-		+
-	Finalizamos dando algunos ejemplos de problemas parabólicos en varias	+
-	dimensiones espaciales, cuyas soluciones explotan en compactos no	+
-	triviales, de dimensión arbitrariamente menor que la del espacio	+
-	ambiente. Para ello deberemos estudiar el soporte de las soluciones de	+
-	ciertos problemas elípticos.	+
-		+
-	En colaboración con Raúl Ferreira (U. Complutense de Madrid), Ján Filo	+
-	(U. Comenius, Eslovaquia), Arturo de Pablo (U. Carlos III de Madrid) y	+
-	Julio D. Rossi (U. de Buenos Aires, Argentina)	+
-		+
-	==Francisco  Montero, Departamento de Bioquímica y Biología Molecular	+
-	I, UCM: "Matemáticas y problemas en bioquímica" 28-II-2008==	+
-		+
-	Resumen: Mi intención es pasar revista a tres problemas: dinámica	+
-	evolutiva y selectiva de sistemas auto-replicativos con error	+
-	(fundamentalmente ecuaciones diferenciales ordinarias y modelos	+
-	estocásticos). tiempos de respuesta en sistemas no lineales	+
-	(deconvoluciones, transformadas de Fourier, etc..,) y análisis	+
-	estequimétricos de redes metabólicas (álgebra de matrices, espacios	+
-	vectoriales convexos, etc..).	+
-		+
-	==Ricardo P. Silva Universidade de São Paulo 6-III-2008  13:00-14:00:	+
-	Parabolic Problems in thin Domains  ==	+
-		+
-	Ricardo P. Silva, Departamento De Matemática, Instituto De Ciências	+
-	Matemáticas e de Computação, Universidade de São Paulo-Campus De São	+
-	Carlos, Caixa Postal 668, 13560-  970 São Carlos Sp, Brazil We study	+
-	semilinear reaction-diffusion problems of the type <center> <math>	+
-	u_t(x,t)  = \Delta u(x,t)+f(u(x,t)),    \Omega \times (0,\infty)	+
-	</math> </center> <center> <math> \frac{\partial u}{\partial \nu}(x,t)	+
-	=  0,  \partial \Omega \times (0,\infty). </math> </center>	+
-		+
-	We develop a abstract theory to obtain the continuity of the	+
-	asymptotic dynamics of <math>(P) </math> under singular perturbations	+
-	of the spatial domain <math>\Omega </math> and we apply that to many	+
-	examples in ''thin domains. ''	+
-		+
-	'''Aula  QB62 '''	+
-		+
-	==Héctor Tejero, Departamento de Bioquímica y Biología Molecular I,	+
-	UCM 13-III-2008 13:00-14:00 Dinámica de cuasiespecies teóricas:	+
-	aproximación determinista ==	+
-		+
-	'''Resumen:''' 'El modelo de Eigen trata de explicar mediante el uso	+
-	de ecuaciones diferenciales ordinarias la dinámica evolutiva de	+
-	especies autorreplicantes sometidas a altas tasas de mutación. De este	+
-	modelo resulta que en estas condiciones las poblaciones son	+
-	distribuciones de mutantes denominadas cuasiespecies. Dicho modelo	+
-	también predice un límite máximo para la tasa de mutación que puede	+
-	soportar una población denominado umbral de error. Finalmente, se	+
-	planteará en qué condiciones se puede producir la extinción de la	+
-	población y cual es su relación con el umbral de error'	+
-		+
-	'''(Atencion al aula QC11) '''	+

---

Última versión de 12:38 27 jun 2022

Contenido 1 Seminarios Cadedif (Curso 21-22) 1.1 23 de Noviembre, Jan Cholewa (U. Silesia, Polonia), 1.2 14 de diciembre, Uwe Brauer (UCM), 1.3 14 de Febrero J. Soria (UCM), 1.4 22 de Febrero Pablo Pedregal (UCLM), Seminario de Depto. 1.5 28 de Febrero Mabel Cuesta (LMPA). Seminario de Depto. 1.6 7 de Marzo 2022. Maya Chhetri (U. Greensboro, USA) Seminario de Depto. 1.7 28 de Marzo 2022. Anibal Rodriguez-Bernal (UCM), 1.8 14 de Junio Joaquin Dominguez de Tena (UCM), 1.9 21 de Junio Manuel Villanueva Pesqueira (U. P. Comillas),

Seminarios Cadedif (Curso 21-22)

El grupo CADEDIF organiza a lo largo del curso un seminario informal del grupo de investigación además de promover Seminarios del Departamento.

23 de Noviembre, Jan Cholewa (U. Silesia, Polonia),

On exponential and global attractors for lattice and reaction-diffusion type problems

14 de diciembre, Uwe Brauer (UCM),

Global existence of a nonlinear wave equation arising from Nordström's theory of gravitation (joint work with Lavi Karp)

Abstract: We show global existence of classical solutions for the nonlinear Nordström theory with a source term and a cosmological constant under the assumption that the source term is small in an appropriate norm, while in some cases no smallness assumption on the initial data is required. In this theory, the gravitational field is described by a single scalar function that satisfies a certain semi-linear wave equation. 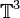We consider spatial periodic deviation from the background metric, that is why we study the semi-linear wave equation on the three-dimensional torus in the Sobolev spaces 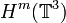. We apply two methods to achieve the existence of global solutions, the first one is by Fourier series, and in the second one, we write the semi-linear wave equation in a non-conventional way as a symmetric hyperbolic system. We also provide results concerning the asymptotic behavior of these solutions and, finally, a blow-up result if the conditions of our global existence theorems are not met.

14 de Febrero J. Soria (UCM),

Operadores maximales: de los espacios Euclídeos a los grafos de Euler

Resumen: Empezando con los resultados clásicos del operador maximal de Hardy-Littlewood en espacios euclídeos:

• acotaciones para diversos tipos de medidas;
• propiedades geométricas;
• aplicaciones a problemas de convergencia de aproximaciones de la identidad o soluciones de EDPs,
• queremos adentrarnos también en algunos avances recientes en contextos discretos, como es el caso de la teoría de grafos.

22 de Febrero Pablo Pedregal (UCLM), Seminario de Depto.

Sobre una nueva condición de frontera

Resumen: Estudiaremos subespacios estrictamente contenidos entre page1imay H¹ El estudio de problemas variacionales sobre tales subespacios conduce a condiciones de frontera especiales entre las clásicas de Dirichlet y Neumann. En concreto, bajo hipótesis apropiadas, se establecerá la existencia de minimizadores y se establecerán las condiciones de optimalidad con especial énfasis en las condiciones óptimas de frontera. La motivación para este estudio procede de los problemas inversos en conductividad en dimensión 3.

28 de Febrero Mabel Cuesta (LMPA). Seminario de Depto.

On a quasilinear elliptic equation with Steklov nonlinear boundary conditions of critical growth (Work in collaboration with Liamidi Leadi)

7 de Marzo 2022. Maya Chhetri (U. Greensboro, USA) Seminario de Depto.

Bifurcation and multiplicity results for elliptic problems with subcritical nonlinearity on the boundary. (University of North Carolina Greensboro)

Abstract: We consider an elliptic problem coupled with a nonlinear boundary condition, involving nonlinearity with superlinear and subcritical growth at infinity, with a bifurcation parameter as a factor. We will discuss the number of positive solutions with respect to the bifurcation parameter depending on the behavior of the nonlinearity at infinity and at zero. We will combine the re-scaling argument with degree theory and bifurcation theory to prove results. This talk is based on a joint work with S. Bandyopadhyay, B. B. Delgado, N. Mavinga and R. Pardo.

28 de Marzo 2022. Anibal Rodriguez-Bernal (UCM),

Principal eigenvalue, maximum principle and stability for nonlocal diffusion equations in metric measure spaces

Resumen: Mostramos resultados generales en espacios de medida métricos que garantizan que se cumpla el principio del máximo, débil y fuerte, para problemas lineales no locales estacionarios y de evolución

14 de Junio Joaquin Dominguez de Tena (UCM),

La ecuación del calor en un dominio exterior

Resumen: Estudiaremos el comportamiento de las soluciones de la ecuación del calor en un dominio exterior, es decir, el complementario de un conjunto compacto en R^N, el cual denominaremos informalmente "agujero".

Empezaremos presentando los principales resultados de existencia de acuerdo a la teoría de semigrupos en los espacios funcionales más habituales: L², L^p, C etc. Estudiaremos el comportamiento asintótico para datos iniciales en Lp, centrándonos en el caso de mayor interés en el cual el dato inicial es integrable. Posteriormente daremos una visión distribucional del problema, donde interpretaremos el "agujero" como una perturbación del problema en todo el espacio. Finalmente, y si queda tiempo, trataremos de "llevar el problema al límite", considerando datos iniciales que admitirán un crecimiento muy grande en el infinito.

21 de Junio Manuel Villanueva Pesqueira (U. P. Comillas),

Homogeneización más allá de la periodicidad

Resumen: A lo largo de los años la teoría de la homogeneización ha sido ampliamente desarrollada para estructuras periódicas. Sin embargo, en ciertas ocasiones las hipótesis clásicas de periodicidad son demasiado restrictivas y surge la necesidad de analizar estructuras más complejas. En particular, en este seminario nos centraremos en la generalización a estructuras con «almost-periodic» heterogeneidades. Mostraremos el método propuesto por S.M. Kozlov en «Averaging differential operators with almost periodic, rapidly oscillating coefficients» y analizaremos las dificultades de adaptarlo a problemas en dominios finos con fronteras oscilantes cuasi-periódicas.