|
|
| (19 ediciones intermedias no se muestran.) |
| Línea 1: |
Línea 1: |
| - | \Delta = 8
| + | __TOC__ |
| | + | <!-- *[[Seminario 2008]] |
| | + | *[[Seminario 2009]] |
| | + | *[[Seminario 2010]] |
| | + | *[[Seminario 2011]] |
| | + | *[[Seminario 2012]] |
| | + | *[[Seminario 2013]] |
| | + | *[[Seminario 2014]] |
| | + | *[[Seminario 2015]] --> |
| | | | |
| - | <math>\int_{-N}^{N} e^x\, dx</math>
| |
| | | | |
| - | <tex> | + | |
| - | \displaystyle\int_{0}^{1}\frac{x^{4}\left(1-x\right)^{4}}{1+x^{2}}dx= | + | ==2007== |
| - | \frac{22}{7}-\pi | + | *'''José Claudio Sabina''' (Universidad de la Laguna). "Estudio de un sistema elíptico bajo condiciones de flujo que dependen de parámetros". Conferencia Inaugural del Departamento de Matemática Aplicada, 02-X-07 |
| - | </tex>
| + | ==2008== |
| | + | *'''Liviu Ignat''' (Instituto de Matemáticas de la Academia de Rumanía (Rumanía). "A nonlocal convection-diffusion equation" 4-III-2008 |
| | + | |
| | + | *'''Pier Domenico Lamberti''' (Dip di Mat Pura e Aplicata Università degli Studi di Padova, Italia) "Spectral stability estimates for elliptic operators in domain perturbation problems", 11-06-08 |
| | + | :'' Abstract:'' We consider the problem of finding estimates for the variation of the eigenvalues of partial differential operators of elliptic type following a domain perturbation. We survey several results and we present some estimates of the type <math> |\lambda_n[\Omega_1]-\lambda_n[\Omega_2 ]|\le c_n \delta (\Omega_1 , \Omega_2),\ \ \ \ n\in {\mathbb{N}}, </math> for some constant <math> c_n </math> depending on <math> n </math>, where <math>\lambda_n[\Omega _1]</math>, <math>\lambda_n[\Omega _2]</math> denote the eigenvalues of operators defined on the open subsets <math>\Omega_1, \Omega_2</math> of <math>{\mathbb{R}}^N</math> respectively, and <math>\delta (\Omega_1 , \Omega_2)</math> is a convenient `measure of vicinity' of <math>\Omega_1</math>, <math>\Omega_2</math> ({e.g.,} Hausdorff distance, Lebesgue measure of <math>\Omega _1\vartriangle \Omega_2</math>, etc.). Joint work with Victor I. Burenkov. |
| | + | *'''Gustavo Cruz Pacheco''' (Universidad Nacional Autónoma de México). "Sistemas Integrables y Propagación de Ondas", 24-VI-2008 |
| | + | |
| | + | *'''Juan Trujillo''' (Universidad de la Laguna) "Modelos Fraccionarios y sus aplicaciones", 11-9-2008 |
| | + | :'' Resumen:'' Este seminario tiene como objetivo principal dar a conocer y motivar a los participantes a preguntarse sobre las posibilidades de esta herramienta como complemento de las técnicas usuales en la modelización de sistemas complejos. En el mismo haremos en primer lugar una introducción formal de los distintos operadores fraccionarios más usuales, destacando algunas de sus propiedades, en especial su no-localidad. Además veremos como estos operadores que carecen de interpretación Geométrica o Física clara cuentan con numerosas ventajas en la modelización de la dinámica de numerosos procesos complejos, deteniéndonos en particular en los procesos de tipo sub y superdifusivos. Por otra parte, veremos mediante ejemplos como este tipo de ecuaciones diferenciales podrían modelar la dinámica de procesos imposible de ser abordados mediante modelos ordinarios lineales o no. Por último, pondremos de manifiesto que la generalización de la Transformada de Fourier (Tranformada Fraccionaria de Fourier) puede jugar un interesante papel en teoría de señales al poder trabajar con una familia de espacios de frecuencias en lugar de uno solo como ocurre en el caso ordinario. No obstante, el desarrollo del seminario será redirigido en función de los intereses de los participantes en el mismo, deteniéndonos con más detalle en aquellos aspectos que pudieran ser de más interés para ellos. |
| | + | |
| | + | *'''Aldo Pratelli''' (IMDEA-matemáticas y Universidad de Pavia, Italia) "Perimeter in the Gauss space: the isoperimetric inequality and its stability" 20-XI-2008, 12:00 Aula 209 |
| | + | :''Abstract:'' We will describe the geometry of <math>\mathbf{R}^n</math> with the Gaussian metric, giving the notion of perimeter and discussing the isoperimetric inequality which holds in this space. We will see an elementary proof of the isoperimetric inequality, together with its stability. |
| | + | |
| | + | ==2009== |
| | + | *'''Waldyr M. Oliva''' (Instituto Superior Técnico de Lisboa y Universidade de Sao Paulo, Brasil) "Reducible Volterra retarded equations with infinite delay" 10-III-2009, 12:00 Aula 209 |
| | + | :''Abstract:''A survey of some results obtained for the reducible case of the Volterra retarded equations with infinite delay. Global questions for this nonlinear system are addressed using the results obtained for the reduced system. Qualitative questions like existence of Liapunov functions and global attractors and, in general, questions regarding the behavior of the global solutions are considered. |
| | + | |
| | + | *'''Peter Kloeden''' (Institut für Mathematik, Johan Wolfgang Goethe Universitat, Frankfurt am Main), "Random attractors and the preservation of synchronization in the presence of noise" 2-VI-2009, Aula 209 |
| | + | :''Abstract:''If two ordinary differential equations with globally asymptotically stable steady state solutions are dissipatively coupled, then the coupled system has a globally asymptotically stable steady state solution which is the cartesion product of the globally asymptotically stable steady state solution of the averaged ordinary differential equation. This property is preserved if the systems are perturbed by additive noise, provided stochastic stationary solutions are used instead of steady state solutions. The formulation and proof require stochastic differential equations and ideas from the theory of random dynamical systems. It will be shown that the synchronization effect is also preserved under the discretization of the systems. Synchronization is also possible modulo factorization by the noise for systems with multiplicative noise. This synchronization effect also occurs in reaction diffusion equations on thin domains on either side of a permeable membrane and is preserved in the presence of additve noise. |
| | + | |
| | + | ==2011== |
| | + | * '''Alejandro Vidal''' (University of Warwick), "Problemas de optimización en espacios de momentos" 21-X-2011, Aula 209 |
| | + | :''Abstract:''En una serie de trabajos en los 70, Fursikov construyó una medida compleja respecto de la cual se tiene regularidad de 3D Navier-Stokes para casi todo dato inicial en un determinado espacio de Hilbert complejo. La idea es resolver una serie de problemas de minimización penalizados, con restricciones dadas por la cadena de momentos asociada a 3DNSE. A través de dos ejemplos sencillos mostraré la técnica empleada por Fursikov, el significado de sus resultados en lo que se refiere al conjunto de datos iniciales para los que 3DNSE es regular y los problemas que nos encontramos a la hora de intentar obtener una medida positiva en vez de una compleja. |
| | + | |
| | + | * '''José Carlos Bellido''' (Universidad de Castilla la Mancha). Un problema de diseño óptimo con restricciones puntuales sobre el estrés. 3-XI-2011. |
| | + | |
| | + | ==2012== |
| | + | |
| | + | |
| | + | * Conferencia Inaugural. '''Alexandre N. Carvalho''' (Universidad de São Paulo, Brasil). Asymptotic behavior of some infinite dimensional non-autonomous dynamical systems. 27 de septiembre de 2012. |
| | + | |
| | + | * '''Eduard Feireisl''' (Academia de Ciencias de la Republica Checa). On weak and strong solutions to the Navier-Stokes system. 19 de octubre de 2012. |
| | + | |
| | + | * '''Hayk Nersisyan''' (BCAM - Basque Center for Applied Mathematics). Controllability of the 3D compressible Euler system. 19 de noviembre de 2012. |
| | + | |
| | + | * '''Jan Cholewa''' (Silesian University, Katowice, Poland). On the equi-exponential attraction and rate of convergence of attractors 5 de deciembre 2012. |
| | + | |
| | + | * '''Luz de Teresa''' (UNAM (México) e ICMAT (España)). Número de condensación y control de ecuaciones parabólicas acopladas. 17 de deciembre 2012. |
| | + | |
| | + | * '''Víctor M. Pérez García''' (Universidad de Castilla-La Mancha). Tumores cerebrales: ¿Pueden las matemáticas ayudar a curarlos? 26 de febrero 2013. |
| | + | |
| | + | * '''Stefanie Sonner''' (BCAM - Basque Center for Applied Mathematics). Attractors for a class of semi-linear degenerate parabolic equations 26 de abril 2013. |
| | + | |
| | + | ==2013== |
| | + | |
| | + | * Conferencia Inaugural 2013: '''Julio Rossi''' ((Universidad de Alicante). Decay estimates for nonlinear nonlocal diffusion problems. Martes 5 de noviembre de 2013 |
| | + | :''Abstract'': We obtain bounds for the decay rate in the <math>L^r</math>-norm for the solutions to a nonlocal and nolinear evolution equation of the form |
| | + | : <math>u_t (x,t) = \int K(x,y) |u(y,t) - u (x,t)|^{p-2} (u(y,t) - u (x,t)) dy.</math> |
| | + | * '''José Antonio Langa''' (Universidad de Sevilla). Dynamical Systems and their attractors under perturbations II Viernes 29 de noviembre. |
| | + | : ''Abstract:'' |
| | + | En estas dos conferencias se dará una vista panoramica al tema de |
| | + | perturbacion de sistemas dinámicos, y atractores tanto para ecuaciones |
| | + | de tipo autónomo como no autonomo. --> |
| | + | * '''Ernesto Nungesser''' (Trinitiy College Dublin). Estabilidad de modelos cosmológicos homogéneos sin constante cosmológica Miercoles 11 de diciembre de 2013. |
| | + | :''Abstract'': Recientemente se han obtenido importantes resultados sobre la estabilidad de soluciones del sistema Einstein-Euler y Einstein-Vlasov con constante cosmológica. En la charla presentaremos resultados obtenidos para soluciones homogéneas del sistema Einstein-Vlasov sin constante cosmológica. Motivaremos el interés de modelos cinéticos en cosmología y como los resultados obtenidos pueden ser generalizados. |
| | + | * '''Pier D. Lamberti''' (University of Padova). Stability for higher order elliptic operators subject to homogeneous boundary conditions on varying domains: Jueves 3 de abril de 2014. Abstract: |
| | + | :'' Abstract'': We consider elliptic partial differential operators of second and higher order, subject to homogeneous boundary conditions on bounded domains of the N-dimensional Euclidean space. We discuss a general theorem ensuring their spectral stability upon perturbation of the underlying domain, in the frame of the so-called E-compact convergence. Applications to the case of the bi-harmonic operator with Dirichlet, Neumann and Intermediate boundary conditions will be considered. |
| | + | |
| | + | ==2014== |
| | + | |
| | + | * '''Eduaro Colorado Heras''' (Universidad Carlos III de Madrid). On the existence of bound and ground states for some coupled nonlinear Schrödinger--Korteweg-de Vries equations: Miércoles 10 de Diciembre. |
| | + | ; ''Abstract'': Along this talk, will be presented some existence results, among others, for the following two systems of coupled nonlinear Schrödinger (NLS) equations, |
| | + | <math> |
| | + | \begin{cases} |
| | + | &\displaystyle -{\rm i}\, \frac{\partial}{\partial t} E_1- \Delta E_1 = \mu_1 |
| | + | |E_1|^2E_1+\beta |E_2|^2E_1,\quad x\in |
| | + | \mathbb{R}^n,\quad t>0\\ |
| | + | & \displaystyle -{\rm i}\, \frac{\partial}{\partial t} E_2- \Delta E_2 = \mu_2 |
| | + | |E_2|^2E_2+\beta |E_1|^2E_2,\quad x\in \mathbb{R}^n,\quad t>0, |
| | + | \end{cases} |
| | + | </math> |
| | + | the coupled parameter |
| | + | <math>\beta\in \mathbb{R}</math>, |
| | + | |
| | + | <math> |
| | + | \lambda_j>0 |
| | + | </math> and |
| | + | <math> |
| | + | \mu_j>0 |
| | + | </math> is for self-focusing in the j-th component of the beam. Also we study the following system of coupled NLS-KdV equations, |
| | + | <!-- <math> |
| | + | \left\{\begin{array}{rcl} if_t + f_{xx} -\beta fg+ |f|^2f& = & 0,\quad x\in \mathbb{R},\quad t>0<br/> g_t +g_{xxx} +gg_x -\frac 12\beta (|f|^2)_x & = & 0,\quad x\in \mathbb{R},\quad t>0, \end{array}\right. |
| | + | </math> --> |
| | + | where <math>f(x,t)\in \mathbb{C}</math>, <math>g(x,t)\in R </math>, <math>\beta\in \mathbb{R}</math> and <math>|f|,\, |g|\to 0$ as $|x|\to \infty</math>. More precisely, we will show existence of positive bound and ground states for the corresponding stationary systems when one looks for solitary wave solutions of (1) and solitary-traveling wave solutions of (2). |
| | + | The results presented in this talk are contained in the following papers. |
| | + | |
| | + | * '''María López Fernández''' (Gran Sasso Science Institute (GSSI), L'Aquila (Italia). Time-stepping methods for convolution equations arising in wave scattering problems. Martes 26 de Mayo |
| | + | : ''Abstract'': We consider the numerical approximation of retarded potentials arising in wave scattering problems. For the temporal approximation we consider a generalization of Lubich's Convolution Quadrature which allows for variable steps. The algorithmic realization of the new method relies on contour integral techniques in the complex plane. Numerical experiments are provided to show the potential of our approach. |
| | + | * '''Alfonso Castro''' (Harvey Mudd College). Indice de Morse y soluciones de un problema elíptico. Jueves 10 de Septiembre |
| | + | : ''Abstract'': Demostramos la existencia de soluciones de problemas variacionales basándonos en las propieddes de los puntos críticos del correspondiente funcional. Analizamos la topología de la variedad de Nehari y su ecuador para concluir la existencia de puntos críticos con índice de Morse aumentado mayor que dos. |
| | + | ==2015== |
| | + | * '''Nsoki Mavinga''' (Swarthmore College (USA)). Steklov eigenproblem and elliptic equations with nonlinear boundary conditions. Miercoles 3 de noviembre |
| | + | : ''Abstract'': |
| | + | We are concerned with the solvability of second order elliptic partial differential equations with nonlinear boundary conditions by imposing asymptotic nonresonance conditions of nonuniform type with respect to the Steklov spectrum on the boundary nonlinearity. We cast the problem in terms of nonlinear compact perturbations of the identity on appropriate trace spaces in order to prove the existence of strong solutions. We obtain a priori estimates for possible solutions to a homotopy on suitable trace spaces and use topological degree arguments. |
| | + | * '''Xavier Cabré''' (Universitat Politècnica de Catalunya). Curves and surfaces with constant nonlocal mean curvature. Jueves 12 de Noviembre |
| | + | |
| | + | <!-- Abstract: |
| | + | |
| | + | We are concerned with hypersurfaces of $\mathbb{R}^N$ with constant nonlocal (or fractional) mean curvature. This is the equation associated to critical points of the fractional perimeter under a volume constraint. Our results are twofold. First we prove the nonlocal analogue of the Alexandrov result characterizing spheres as the only closed embedded hypersurfaces in $\mathbb{R}^N$ with constant mean curvature. Here we use the moving planes method. Our second result establishes the existence of periodic bands or ''cylinders'' in $\mathbb{R}^2$ with constant nonlocal mean curvature and bifurcating from a straight band. These are Delaunay type bands in the nonlocal setting. Here we use a Lyapunov-Schmidt procedure for a quasilinear type fractional elliptic equation. (This is joint work with Mouhamed M. Fall, Joan Solà-Morales, and Tobias Weth) --> |
| | + | * '''Jaime Ortega''' (University of Chile, Santiago). Some ideas on inverse problems in fluid mechanics. Miercoles 18 de noviembre |
| | + | <!-- Abstract: |
| | + | |
| | + | In the last years, Inverse problems became and interesting area, due to the large number of applications, for example in medicine, mining, earth sciences, oceanography, among others. In this talk we will focus in the study of inverse problems related with fluid mechanics. We will present a review of several results in viscous and inviscid fluids, related with the analogous well known Calderon’s Problems and with the called geometric Inverse problems. Finally we will discuss some open problems. --> |
| | + | |
| | + | * '''Alessandra Lunardi''' (University of Parma). Surface measures in Banach spaces. 25 Feb 2016. |
| | + | <!-- Abstract: |
| | + | Let X be a Banach space endowed with a probability Borel measure m. I will describe different approaches for the construction of surface measures associated to m, and related integration by parts formulae on smooth enough subsets of X. The available literature deals mainly with non-degenerate Gaussian measures in separable Banach spaces. In that case, integration by parts formulae for smooth functions are similar (as far as possible) to the finite dimensional case. They may be extended to Sobolev functions since a trace theory for Sobolev functions on smooth surfaces is available. --> |
| | + | |
| | + | * '''Rafael Orive''' (ICMAT). Análisis de fluidos incompresibles en medios porosos spaces. 15 Marzo 2016. |
| | + | |
| | + | <!-- Abstract: |
| | + | En este seminario hablaremos sobre las soluciones del sistema de ecuaciones que involucran la transferencia del calor con un término de disipación fraccionario en un fluido incompresible en un medio poroso (DPM). Este sistema se escribe del siguiente modo |
| | + | |
| | + | \begin{eqnarray*} & &\displaystyle\frac{\partial T}{\partial t}+v\cdot\nabla T=-\nu\Lambda^\alpha T,\\ & &\label{darcy} v=-\left(\nabla p+\gamma T\right),\\ & & \label{incom} \hbox{div}\, v=0, \end{eqnarray*} |
| | + | para $\nu>0$, y $\Lambda^\alpha \equiv (-\Delta)^{\alpha/2}$. |
| | + | |
| | + | Se considera $0\leq \alpha \leq 2$ . El caso $\alpha = 1$ se conoce como crítico, $1<\alpha \leq 2$ es subcrítico y caso $0\leq \alpha < 1$ supercrítico. Trataremos distintas propiedades de sus soluciones dependiendo de este valor. En particular, mostraremos cómo propiedades de sus soluciones son compartidas con otros modelos de sistemas resultantes de la mecánica de fluidos, como las ecuaciones de Euler, la ecuación de Burgers, las ecuaciones quasigeostróficas, las ecuaciones de la magneto hidrodinámica o la ecuación de Boussinesq. |
| | + | |
| | + | Este trabajo ha resultado de la colaboración con A. Castro, D. Córdoba, F. Gancedo, R. Granero, R. Miclea y C. Niche. --> |
| | + | * '''Jorge Cossio''' (Universidad Nacional de Colombia Sede Medellín). Existence And Multiplicity Results for some quasilinear elliptic problems 5 Abril 2016 |
| | + | |
| | + | <!-- Abstract: |
| | + | |
| | + | In this talk we study the existence of solutions for the quasilinear elliptic boundary value problem |
| | + | |
| | + | $$\begin{aligned} \label{PL} \left\{\begin{array}{rl} \Delta _pu + f(u)& = 0 \qquad \hbox{in} \ \ \ \Omega,\\ u & = 0 \qquad \hbox{on} \ \ \partial \Omega, \end{array}\right.\end{aligned}$$ |
| | + | |
| | + | where $\Delta _p u=$ div$(|\nabla u|^{p-2}\nabla u)$ is the $p$-Laplace operator, $p>1$, $\Omega \subset \mathbb{R}^N$ ($N \ge 2$) is a bounded and smooth domain, and $f :\mathbb{R} \to \mathbb{R}$ is a nonlinear function such that $f(0)=0$. |
| | + | First we present some results concerning the existence of multiple radial solutions for problem ([PL]), when the nonlinearity is either p-asymptotically linear at infinity or p-asymptotically superlinear at the origin. The main tools that we use are bifurcation theory and the shooting method. Additionally, we prove the existence of multiple solutions for problem ([PL]), when the $p$-derivative at zero and the p-derivative at infinity are greater than the first eigenvalue of the $p$-Laplace operator. We extend a result due to J. Cossio, S. Herrón, and C. Vélez --> |
| | + | |
| | + | |
| | + | Smith wrote the definitive book on yammering. |
| | + | {{ref|Smith2000|Smith 2000}} |
| | + | |
| | + | ==Bibliography== |
| | + | *{{note|Smith2000}}, Smith 2000, "A book about yammering". |
En estas dos conferencias se dará una vista panoramica al tema de
perturbacion de sistemas dinámicos, y atractores tanto para ecuaciones
de tipo autónomo como no autonomo. -->
We are concerned with the solvability of second order elliptic partial differential equations with nonlinear boundary conditions by imposing asymptotic nonresonance conditions of nonuniform type with respect to the Steklov spectrum on the boundary nonlinearity. We cast the problem in terms of nonlinear compact perturbations of the identity on appropriate trace spaces in order to prove the existence of strong solutions. We obtain a priori estimates for possible solutions to a homotopy on suitable trace spaces and use topological degree arguments.

![|\lambda_n[\Omega_1]-\lambda_n[\Omega_2 ]|\le c_n \delta (\Omega_1 , \Omega_2),\ \ \ \ n\in {\mathbb{N}},](/wiki/images/math/9/9/6/996f86cab511943d885c6461279eeb8d.png) for some constant
for some constant 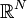 respectively, and
respectively, and 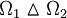 , etc.). Joint work with Victor I. Burenkov.
, etc.). Joint work with Victor I. Burenkov.
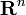 with the Gaussian metric, giving the notion of perimeter and discussing the isoperimetric inequality which holds in this space. We will see an elementary proof of the isoperimetric inequality, together with its stability.
with the Gaussian metric, giving the notion of perimeter and discussing the isoperimetric inequality which holds in this space. We will see an elementary proof of the isoperimetric inequality, together with its stability.
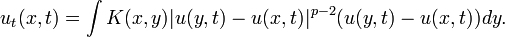
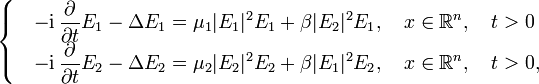 the coupled parameter
the coupled parameter
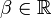 ,
,
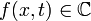 ,
, 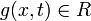 ,
, 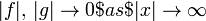 . More precisely, we will show existence of positive bound and ground states for the corresponding stationary systems when one looks for solitary wave solutions of (1) and solitary-traveling wave solutions of (2).
The results presented in this talk are contained in the following papers.
. More precisely, we will show existence of positive bound and ground states for the corresponding stationary systems when one looks for solitary wave solutions of (1) and solitary-traveling wave solutions of (2).
The results presented in this talk are contained in the following papers.