De Cadedif
(Diferencias entre revisiones)
|
|
| Línea 6: |
Línea 6: |
| | &\displaystyle -{\rm i}\, \frac{\partial}{\partial t} E_1- \Delta E_1 = \mu_1 | | &\displaystyle -{\rm i}\, \frac{\partial}{\partial t} E_1- \Delta E_1 = \mu_1 |
| | |E_1|^2E_1+\beta |E_2|^2E_1,\quad x\in | | |E_1|^2E_1+\beta |E_2|^2E_1,\quad x\in |
| - | \mathbb{R}^n,\quad t>0\\ | + | \mathbb{R}^n,\quad t>0\\[0.3cm] |
| | & \displaystyle -{\rm i}\, \frac{\partial}{\partial t} E_2- \Delta E_2 = \mu_2 | | & \displaystyle -{\rm i}\, \frac{\partial}{\partial t} E_2- \Delta E_2 = \mu_2 |
| | |E_2|^2E_2+\beta |E_1|^2E_2,\quad x\in \mathbb{R}^n,\quad t>0, | | |E_2|^2E_2+\beta |E_1|^2E_2,\quad x\in \mathbb{R}^n,\quad t>0, |
Última versión de 14:12 24 abr 2016
![\begin{cases}
&\displaystyle -{\rm i}\, \frac{\partial}{\partial t} E_1- \Delta E_1 = \mu_1
|E_1|^2E_1+\beta |E_2|^2E_1,\quad x\in
\mathbb{R}^n,\quad t>0\\[0.3cm]
& \displaystyle -{\rm i}\, \frac{\partial}{\partial t} E_2- \Delta E_2 = \mu_2
|E_2|^2E_2+\beta |E_1|^2E_2,\quad x\in \mathbb{R}^n,\quad t>0,
\end{cases}](/wiki/images/math/5/6/a/56a4655187b3323c785c77cf4763adad.png)
the coupled parameter
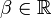 ,
,