De Cadedif
(Diferencias entre revisiones)
|
|
| Línea 1: |
Línea 1: |
| - | = Seminarios Cadedif = | + | = Seminarios Cadedif (Curso 21-22) = |
| | El grupo CADEDIF organiza a lo largo del curso un seminario informal del grupo de investigación además de promover Seminarios del | | El grupo CADEDIF organiza a lo largo del curso un seminario informal del grupo de investigación además de promover Seminarios del |
| | Departamento. | | Departamento. |
| | | | |
| - | En el curso 21–22 los seminarios celebrados son:
| |
| | | | |
| - | == 23 de Noviembre 2021, Jan Cholewa (U. Silesia, Polonia), == | + | |
| | + | == 23 de Noviembre, Jan Cholewa (U. Silesia, Polonia), == |
| | On exponential and global attractors for lattice and reaction-diffusion type problems | | On exponential and global attractors for lattice and reaction-diffusion type problems |
| | | | |
| - | == 14 de diciembre 2021, Uwe Brauer (UCM), == | + | == 14 de diciembre, Uwe Brauer (UCM), == |
| | Global existence of a nonlinear wave equation arising from Nordström's theory of gravitation (joint work with Lavi Karp) | | Global existence of a nonlinear wave equation arising from Nordström's theory of gravitation (joint work with Lavi Karp) |
| | | | |
| Línea 15: |
Línea 15: |
| | required. In this theory, the gravitational field is described by a single scalar function that satisfies a certain semi-linear wave equation. | | required. In this theory, the gravitational field is described by a single scalar function that satisfies a certain semi-linear wave equation. |
| | We consider spatial periodic deviation from the background metric, that is why we study the semi-linear wave equation on the three-dimensional | | We consider spatial periodic deviation from the background metric, that is why we study the semi-linear wave equation on the three-dimensional |
| - | torus \(\mathbb T^3\) in the Sobolev spaces \(H^m(\mathbb T^3)\). We apply two methods to achieve the existence of global solutions, the first one | + | torus <math>\mathbb T^3</math> in the Sobolev spaces <math>H^m(\mathbb T^3)</math>. We apply two methods to achieve the existence of global solutions, the first one |
| | is by Fourier series, and in the second one, we write the semi-linear wave equation in a non-conventional way as a symmetric hyperbolic | | is by Fourier series, and in the second one, we write the semi-linear wave equation in a non-conventional way as a symmetric hyperbolic |
| | system. We also provide results concerning the asymptotic behavior of these solutions and, finally, a blow-up result if the conditions of our | | system. We also provide results concerning the asymptotic behavior of these solutions and, finally, a blow-up result if the conditions of our |
| | global existence theorems are not met. | | global existence theorems are not met. |
| | | | |
| - | == 14 de Febrero 2022, J. Soria (UCM), == | + | == 14 de Febrero J. Soria (UCM), == |
| | Operadores maximales: de los espacios Euclídeos a los grafos de Euler | | Operadores maximales: de los espacios Euclídeos a los grafos de Euler |
| | | | |
| Línea 33: |
Línea 33: |
| | * queremos adentrarnos también en algunos avances recientes en contextos discretos, como es el caso de la teoría de grafos. | | * queremos adentrarnos también en algunos avances recientes en contextos discretos, como es el caso de la teoría de grafos. |
| | | | |
| - | == 22 de Febrero 2022, Pablo Pedregal (UCLM), Seminario de Depto. == | + | == 22 de Febrero Pablo Pedregal (UCLM), Seminario de Depto. == |
| | Sobre una nueva condición de frontera | | Sobre una nueva condición de frontera |
| | | | |
| Línea 60: |
Línea 60: |
| | para problemas lineales no locales estacionarios y de evolución | | para problemas lineales no locales estacionarios y de evolución |
| | | | |
| - | == 14 de Junio 2022, Joaquin Dominguez de Tena (UCM), == | + | == 14 de Junio Joaquin Dominguez de Tena (UCM), == |
| | La ecuación del calor en un dominio exterior | | La ecuación del calor en un dominio exterior |
| | | | |
| - | '''Resumen:''' Estudiaremos el comportamiento de las soluciones de la ecuación del calor en un dominio exterior, es decir, el complementario de un | + | '''Resumen:''' Estudiaremos el comportamiento de las soluciones de la ecuación del calor en un dominio exterior, es decir, el complementario de un conjunto compacto en R<sup>N</sup>, el cual denominaremos informalmente "agujero". |
| - | conjunto compacto en R<sup>N</sup>, el cual denominaremos informalmente "agujero". | + | |
| | | | |
| - | Empezaremos presentando los principales resultados de existencia de acuerdo a la teoría de semigrupos en los espacios funcionales más | + | Empezaremos presentando los principales resultados de existencia de acuerdo a la teoría de semigrupos en los espacios funcionales más habituales: L<sup>2</sup>, L<sup>p</sup>, C etc. Estudiaremos el comportamiento asintótico para datos iniciales en Lp, centrándonos en el caso de mayor interés en el cual el dato inicial es integrable. Posteriormente daremos una visión distribucional del problema, donde interpretaremos el "agujero" como una perturbación del problema en todo el espacio. Finalmente, y si queda tiempo, trataremos de "llevar el problema al límite", considerando datos iniciales que admitirán un crecimiento muy grande en el infinito. |
| - | habituales: L<sup>2</sup>, L<sup>p</sup>, C etc. Estudiaremos el comportamiento asintótico para datos iniciales en Lp, centrándonos en el caso de mayor interés en | + | |
| - | el cual el dato inicial es integrable. Posteriormente daremos una visión distribucional del problema, donde interpretaremos el "agujero" como | + | |
| - | una perturbación del problema en todo el espacio. Finalmente, y si queda tiempo, trataremos de "llevar el problema al límite", considerando | + | |
| - | datos iniciales que admitirán un crecimiento muy grande en el infinito. | + | |
| | | | |
| - | == 21 de Junio 2022, Manuel Villanueva Pesqueira (U. P. Comillas), == | + | == 21 de Junio Manuel Villanueva Pesqueira (U. P. Comillas), == |
| | Homogeneización más allá de la periodicidad | | Homogeneización más allá de la periodicidad |
| | | | |
| - | Resumen: A lo largo de los años la teoría de la homogeneización ha sido ampliamente desarrollada para estructuras periódicas. Sin embargo, en | + | Resumen: A lo largo de los años la teoría de la homogeneización ha sido ampliamente desarrollada para estructuras periódicas. Sin embargo, en ciertas ocasiones las hipótesis clásicas de periodicidad son demasiado restrictivas y surge la necesidad de analizar estructuras más complejas. En particular, en este seminario nos centraremos en la generalización a estructuras con «almost-periodic» heterogeneidades. |
| - | ciertas ocasiones las hipótesis clásicas de periodicidad son demasiado restrictivas y surge la necesidad de analizar estructuras más | + | Mostraremos el método propuesto por S.M. Kozlov en «Averaging differential operators with almost periodic, rapidly oscillating coefficients» y analizaremos las dificultades de adaptarlo a problemas en dominios finos con fronteras oscilantes cuasi-periódicas. |
| - | complejas. En particular, en este seminario nos centraremos en la generalización a estructuras con «almost-periodic» heterogeneidades. | + | |
| - | | + | |
| - | Mostraremos el método propuesto por S.M. Kozlov en «Averaging differential operators with almost periodic, rapidly oscillating coefficients» | + | |
| - | y analizaremos las dificultades de adaptarlo a problemas en dominios finos con fronteras oscilantes cuasi-periódicas. | + | |
Revisión de 15:51 20 jun 2022
Contenido
- 1 Seminarios Cadedif (Curso 21-22)
- 1.1 23 de Noviembre, Jan Cholewa (U. Silesia, Polonia),
- 1.2 14 de diciembre, Uwe Brauer (UCM),
- 1.3 14 de Febrero J. Soria (UCM),
- 1.4 22 de Febrero Pablo Pedregal (UCLM), Seminario de Depto.
- 1.5 28 de Febrero 2022. Seminario de Depto. Mabel Cuesta, LMPA,
- 1.6 7 de Marzo 2022. Seminario de Depto. Maya Chhetri,
- 1.7 28 de Marzo 2022. Anibal Rodriguez-Bernal (UCM),
- 1.8 14 de Junio Joaquin Dominguez de Tena (UCM),
- 1.9 21 de Junio Manuel Villanueva Pesqueira (U. P. Comillas),
|
Seminarios Cadedif (Curso 21-22)
El grupo CADEDIF organiza a lo largo del curso un seminario informal del grupo de investigación además de promover Seminarios del
Departamento.
23 de Noviembre, Jan Cholewa (U. Silesia, Polonia),
On exponential and global attractors for lattice and reaction-diffusion type problems
14 de diciembre, Uwe Brauer (UCM),
Global existence of a nonlinear wave equation arising from Nordström's theory of gravitation (joint work with Lavi Karp)
Abstract: We show global existence of classical solutions for the nonlinear Nordström theory with a source term and a cosmological constant
under the assumption that the source term is small in an appropriate norm, while in some cases no smallness assumption on the initial data is
required. In this theory, the gravitational field is described by a single scalar function that satisfies a certain semi-linear wave equation.
We consider spatial periodic deviation from the background metric, that is why we study the semi-linear wave equation on the three-dimensional
torus 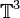 in the Sobolev spaces
in the Sobolev spaces 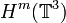 . We apply two methods to achieve the existence of global solutions, the first one
is by Fourier series, and in the second one, we write the semi-linear wave equation in a non-conventional way as a symmetric hyperbolic
system. We also provide results concerning the asymptotic behavior of these solutions and, finally, a blow-up result if the conditions of our
global existence theorems are not met.
. We apply two methods to achieve the existence of global solutions, the first one
is by Fourier series, and in the second one, we write the semi-linear wave equation in a non-conventional way as a symmetric hyperbolic
system. We also provide results concerning the asymptotic behavior of these solutions and, finally, a blow-up result if the conditions of our
global existence theorems are not met.
14 de Febrero J. Soria (UCM),
Operadores maximales: de los espacios Euclídeos a los grafos de Euler
Resumen: Empezando con los resultados clásicos del operador maximal de Hardy-Littlewood en espacios euclídeos:
- acotaciones para diversos tipos de medidas;
- aplicaciones a problemas de convergencia de aproximaciones de la identidad o soluciones de EDPs,
- queremos adentrarnos también en algunos avances recientes en contextos discretos, como es el caso de la teoría de grafos.
22 de Febrero Pablo Pedregal (UCLM), Seminario de Depto.
Sobre una nueva condición de frontera
Resumen: Estudiaremos subespacios estrictamente contenidos entre page1imay H1
El estudio de problemas variacionales sobre tales subespacios conduce a condiciones de frontera especiales entre las clásicas de Dirichlet
y Neumann. En concreto, bajo hipótesis apropiadas, se establecerá la existencia de minimizadores y se establecerán las condiciones
de optimalidad con especial énfasis en las condiciones óptimas de frontera. La motivación para este estudio procede de los problemas inversos
en conductividad en dimensión 3.
28 de Febrero 2022. Seminario de Depto. Mabel Cuesta, LMPA,
On a quasilinear elliptic equation with Steklov nonlinear boundary conditions of critical growth (Work in collaboration with Liamidi Leadi)
7 de Marzo 2022. Seminario de Depto. Maya Chhetri,
Bifurcation and multiplicity results for elliptic problems with subcritical nonlinearity on the boundary.
(University of North Carolina Greensboro)
Abstract: We consider an elliptic problem coupled with a nonlinear boundary condition, involving nonlinearity with superlinear and subcritical
growth at infinity, with a bifurcation parameter as a factor. We will discuss the number of positive solutions with respect to the bifurcation
parameter depending on the behavior of the nonlinearity at infinity and at zero. We will combine the re-scaling argument with degree theory
and bifurcation theory to prove results. This talk is based on a joint work with S. Bandyopadhyay, B. B. Delgado, N. Mavinga and R. Pardo.
28 de Marzo 2022. Anibal Rodriguez-Bernal (UCM),
Principal eigenvalue, maximum principle and stability for nonlocal diffusion equations in metric measure spaces
Resumen: Mostramos resultados generales en espacios de medida métricos que garantizan que se cumpla el principio del máximo, débil y fuerte,
para problemas lineales no locales estacionarios y de evolución
14 de Junio Joaquin Dominguez de Tena (UCM),
La ecuación del calor en un dominio exterior
Resumen: Estudiaremos el comportamiento de las soluciones de la ecuación del calor en un dominio exterior, es decir, el complementario de un conjunto compacto en RN, el cual denominaremos informalmente "agujero".
Empezaremos presentando los principales resultados de existencia de acuerdo a la teoría de semigrupos en los espacios funcionales más habituales: L2, Lp, C etc. Estudiaremos el comportamiento asintótico para datos iniciales en Lp, centrándonos en el caso de mayor interés en el cual el dato inicial es integrable. Posteriormente daremos una visión distribucional del problema, donde interpretaremos el "agujero" como una perturbación del problema en todo el espacio. Finalmente, y si queda tiempo, trataremos de "llevar el problema al límite", considerando datos iniciales que admitirán un crecimiento muy grande en el infinito.
21 de Junio Manuel Villanueva Pesqueira (U. P. Comillas),
Homogeneización más allá de la periodicidad
Resumen: A lo largo de los años la teoría de la homogeneización ha sido ampliamente desarrollada para estructuras periódicas. Sin embargo, en ciertas ocasiones las hipótesis clásicas de periodicidad son demasiado restrictivas y surge la necesidad de analizar estructuras más complejas. En particular, en este seminario nos centraremos en la generalización a estructuras con «almost-periodic» heterogeneidades.
Mostraremos el método propuesto por S.M. Kozlov en «Averaging differential operators with almost periodic, rapidly oscillating coefficients» y analizaremos las dificultades de adaptarlo a problemas en dominios finos con fronteras oscilantes cuasi-periódicas.
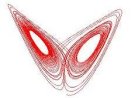

 in the Sobolev spaces
in the Sobolev spaces 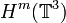 . We apply two methods to achieve the existence of global solutions, the first one
is by Fourier series, and in the second one, we write the semi-linear wave equation in a non-conventional way as a symmetric hyperbolic
system. We also provide results concerning the asymptotic behavior of these solutions and, finally, a blow-up result if the conditions of our
global existence theorems are not met.
. We apply two methods to achieve the existence of global solutions, the first one
is by Fourier series, and in the second one, we write the semi-linear wave equation in a non-conventional way as a symmetric hyperbolic
system. We also provide results concerning the asymptotic behavior of these solutions and, finally, a blow-up result if the conditions of our
global existence theorems are not met.